Affine scheme
A generalization of the concept of an affine variety, which plays the role of a local object in the theory of schemes. Let 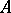 be a commutative ring with a unit. An affine scheme consists of a topological space
be a commutative ring with a unit. An affine scheme consists of a topological space 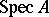 and a sheaf of rings
and a sheaf of rings 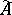 on
on 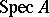 . Here,
. Here, 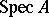 is the set of all prime ideals of
is the set of all prime ideals of 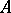 (called the points of the affine scheme), provided with the Zariski topology (or, which is the same, with the spectral topology), in which the basis of open sets is constituted by the subsets
(called the points of the affine scheme), provided with the Zariski topology (or, which is the same, with the spectral topology), in which the basis of open sets is constituted by the subsets 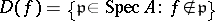 , where
, where 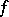 runs through the elements of
runs through the elements of 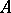 . The sheaf of local rings
. The sheaf of local rings 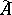 is defined by the condition
is defined by the condition 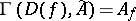 , where
, where 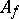 is the localization of the ring
is the localization of the ring 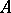 with respect to the multiplicative system
with respect to the multiplicative system 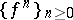 , cf. Localization in a commutative algebra.
, cf. Localization in a commutative algebra.
Affine schemes were first introduced by A. Grothendieck [1], who created the theory of schemes. A scheme is a ringed space which is locally isomorphic to an affine scheme.
An affine scheme 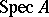 is called Noetherian (integral, reduced, normal, or regular, respectively) if the ring
is called Noetherian (integral, reduced, normal, or regular, respectively) if the ring 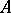 is Noetherian (integral, without nilpotents, integrally closed, or regular, respectively). An affine scheme is called connected (irreducible, discrete, or quasi-compact, respectively) if the topological space
is Noetherian (integral, without nilpotents, integrally closed, or regular, respectively). An affine scheme is called connected (irreducible, discrete, or quasi-compact, respectively) if the topological space 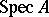 also has these properties. The space
also has these properties. The space 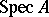 of an affine scheme is always compact (and usually not Hausdorff).
of an affine scheme is always compact (and usually not Hausdorff).
The affine schemes form a category if the morphisms of these schemes, considered as locally ringed spaces, are considered as morphisms of affine schemes. Each homomorphism of rings 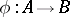 defines a morphism of affine schemes:
defines a morphism of affine schemes: 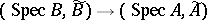 , consisting of the continuous mapping
, consisting of the continuous mapping 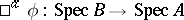 (
(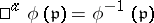 for
for  ), and a homomorphism of sheaves of rings
), and a homomorphism of sheaves of rings 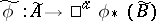 , which transforms the section
, which transforms the section 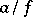 of the sheaf
of the sheaf 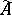 over the set
over the set 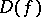 into the section
into the section 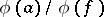 . The morphisms of an arbitrary scheme
. The morphisms of an arbitrary scheme 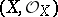 into an affine scheme (
into an affine scheme (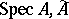 ) (which are also called
) (which are also called 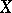 -valued points of
-valued points of 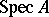 ) are in a one-to-one correspondence with the homomorphisms of rings
) are in a one-to-one correspondence with the homomorphisms of rings 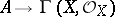 ; thus, the correspondence
; thus, the correspondence 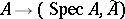 is a contravariant functor from the category of commutative rings with a unit into the category of affine schemes, which establishes an anti-equivalence of these categories. In particular, in the category of affine schemes there are finite direct sums and fibre products, dual to the constructions of the direct sum and the tensor product of rings. The morphisms of affine schemes which correspond to surjective homomorphisms of rings are called closed imbeddings of affine schemes.
is a contravariant functor from the category of commutative rings with a unit into the category of affine schemes, which establishes an anti-equivalence of these categories. In particular, in the category of affine schemes there are finite direct sums and fibre products, dual to the constructions of the direct sum and the tensor product of rings. The morphisms of affine schemes which correspond to surjective homomorphisms of rings are called closed imbeddings of affine schemes.
The most important examples of affine schemes are affine varieties; other examples are affine group schemes (cf. Group scheme).
In a manner similar to the construction of the sheaf  it is possible to construct, for any
it is possible to construct, for any 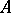 -module
-module 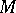 , a sheaf of
, a sheaf of 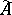 -modules
-modules 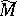 on
on 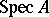 for which
for which
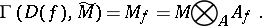 |
Such sheaves are called quasi-coherent. The category of 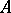 -modules is equivalent to the category of quasi-coherent sheaves of
-modules is equivalent to the category of quasi-coherent sheaves of 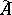 -modules on
-modules on 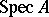 ; projective modules correspond to locally free sheaves. The cohomology spaces of quasi-coherent sheaves over an affine scheme are described by Serre's theorem:
; projective modules correspond to locally free sheaves. The cohomology spaces of quasi-coherent sheaves over an affine scheme are described by Serre's theorem:
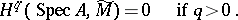 |
The converse of this theorem (Serre's criterion for affinity) states that if 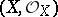 is a compact separable scheme, and if
is a compact separable scheme, and if 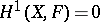 for any quasi-coherent sheaf of
for any quasi-coherent sheaf of 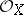 -modules
-modules 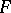 , then
, then 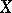 is an affine scheme. Other criteria for affinity also exist [1], [4].
is an affine scheme. Other criteria for affinity also exist [1], [4].
References
| [1] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" Publ. Math. IHES , 4 (1960) |
| [2] | J. Dieudonné, "Algebraic geometry" Adv. in Math. , 1 (1969) pp. 233–321 |
| [3] | Yu.I. Manin, "Lectures on algebraic geometry" , 1 , Moscow (1970) (In Russian) |
| [4] | J. Goodman, R. Hartshorne, "Schemes with finite-dimensional cohomology groups" Amer. J. Math. , 91 (1969) pp. 258–266 |
Comments
Reference [a1] is, of course, standard. It replaces [3]. An alternative to [1] is [a2].
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [a2] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971) |
Affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_scheme&oldid=15083