Affine design
Let  be a resolvable
be a resolvable 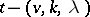 -design (see Tactical configuration), that is, the block set of
-design (see Tactical configuration), that is, the block set of 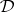 is partitioned into parallel classes each of which in turn partitions the point set
is partitioned into parallel classes each of which in turn partitions the point set 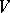 .
. 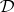 is called affine, or affine resolvable, if there exists a constant
is called affine, or affine resolvable, if there exists a constant 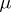 such that any two non-parallel blocks intersect in exactly
such that any two non-parallel blocks intersect in exactly 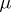 points. For proofs of the results stated below, see [a1].
points. For proofs of the results stated below, see [a1].
The affine  -designs are precisely the nets, see Net (in finite geometry), and the affine
-designs are precisely the nets, see Net (in finite geometry), and the affine  -designs coincide with the Hadamard
-designs coincide with the Hadamard  -designs, that is, the
-designs, that is, the 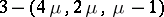 -designs, cf. Tactical configuration. There are no non-trivial affine
-designs, cf. Tactical configuration. There are no non-trivial affine 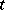 -designs with
-designs with 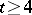 . Thus, the most interesting case is that of affine
. Thus, the most interesting case is that of affine  -designs, which are often simply called affine designs. Any affine
-designs, which are often simply called affine designs. Any affine 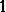 -design satisfies the inequality
-design satisfies the inequality 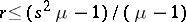 , where
, where  denotes the number of blocks through a point and where
denotes the number of blocks through a point and where  denotes the number of blocks in a parallel class. Moreover, equality holds in this inequality if and only the
denotes the number of blocks in a parallel class. Moreover, equality holds in this inequality if and only the 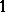 -design is an (affine)
-design is an (affine)  -design. Any resolvable
-design. Any resolvable  -design satisfies the inequality
-design satisfies the inequality 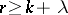 , and equality holds if and only the design is affine. In this case, all parameters of
, and equality holds if and only the design is affine. In this case, all parameters of 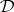 may be written in terms of the two parameters
may be written in terms of the two parameters  and
and 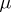 , as follows:
, as follows:
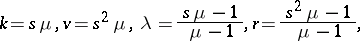 |
and the design is denoted by 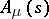 .
.
The outstanding problem in this area is to characterize the possible pairs 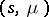 for which an
for which an 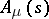 exists. The only known pairs to date (2001) are those with
exists. The only known pairs to date (2001) are those with 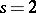 and the pairs of the form
and the pairs of the form 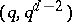 for some prime power
for some prime power 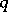 and some integer
and some integer 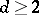 . The case
. The case 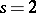 corresponds to Hadamard
corresponds to Hadamard  -designs, i.e.
-designs, i.e. 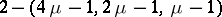 -designs; any such design extends uniquely to a Hadamard
-designs; any such design extends uniquely to a Hadamard  -design, and existence — which is equivalent to that of an Hadamard matrix of order
-design, and existence — which is equivalent to that of an Hadamard matrix of order 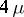 — is conjectured for all values of
— is conjectured for all values of 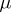 . The classical examples for the second case are the affine designs
. The classical examples for the second case are the affine designs 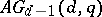 formed by the points and hyperplanes of the
formed by the points and hyperplanes of the 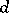 -dimensional finite affine spaces
-dimensional finite affine spaces 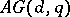 over the Galois field
over the Galois field 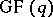 of order
of order 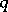 (so
(so 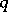 is a prime power here; cf. also Affine space). As to the case
is a prime power here; cf. also Affine space). As to the case 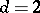 , a design
, a design 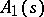 is just an affine plane of order
is just an affine plane of order  , see also Plane.
, see also Plane.
In general, an affine design cannot be characterized just by its parameters. For instance, the number of non-isomorphic designs with the same parameters as 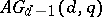 grows exponentially with a growth rate of at least
grows exponentially with a growth rate of at least  , where
, where 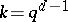 . Hence, it is desirable to characterize the designs
. Hence, it is desirable to characterize the designs 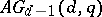 among the affine or resolvable designs. For instance, by Dembowski's theorem, a resolvable design
among the affine or resolvable designs. For instance, by Dembowski's theorem, a resolvable design 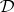 with
with 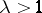 and
and 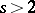 in which every line (that is, the intersection of all blocks through two given points) meets every non-parallel block is isomorphic to some
in which every line (that is, the intersection of all blocks through two given points) meets every non-parallel block is isomorphic to some 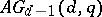 ; the same conclusion holds if
; the same conclusion holds if 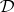 admits an automorphism group which is transitive on ordered triples of non-collinear points. See [a1], Sec. XII.3, for proofs and further characterizations. In particular, there is a wealth of results characterizing the classical affine planes
admits an automorphism group which is transitive on ordered triples of non-collinear points. See [a1], Sec. XII.3, for proofs and further characterizations. In particular, there is a wealth of results characterizing the classical affine planes  and other interesting classes of affine planes; for example, a result of Y. Hiramine [a2] states that any finite affine plane that admits a collineation group acting primitively on points is a translation plane (cf. Plane; Primitive group of permutations). Detailed studies of translation planes may be found in [a3] and [a4].
and other interesting classes of affine planes; for example, a result of Y. Hiramine [a2] states that any finite affine plane that admits a collineation group acting primitively on points is a translation plane (cf. Plane; Primitive group of permutations). Detailed studies of translation planes may be found in [a3] and [a4].
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1999) (Edition: Second) |
| [a2] | Y. Hiramine, "Affine planes with primitive collineation groups" J. Algebra , 128 (1990) pp. 366–383 |
| [a3] | M.J. Kallaher, "Affine planes with transitive collineation groups" , North-Holland (1981) |
| [a4] | H. Lüneburg, "Translation planes" , Springer (1980) |
Affine design. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_design&oldid=15782