Abstract Cauchy problem
The condensed formulation of a Cauchy problem (as phrased by J. Hadamard) in an infinite-dimensional topological vector space. While it seems to have arisen between the two World Wars (F. Browder in [a2], Foreword), it was apparently introduced as such by E. Hille in 1952, [a2], Sec. 1.7.
Narrowly, but loosely speaking, the abstract Cauchy problem consists in solving a linear abstract differential equation (cf. also Differential equation, abstract) or abstract evolution equation subject to an initial condition. More precise explanations slightly differ from textbook to textbook [a2], [a5]. Following A. Pazy [a5], given a linear operator  on a Banach space
on a Banach space  with domain
with domain  and given an element
and given an element  , one tries to solve
, one tries to solve
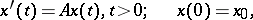 |
i.e., one looks for a continuous function  on
on  such that
such that  is differentiable on
is differentiable on 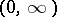 ,
, 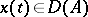 for all
for all  , and
, and 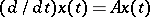 for all
for all 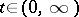 .
.
Since  is required to be continuous at
is required to be continuous at  , the Cauchy problem can only be solved for
, the Cauchy problem can only be solved for 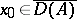 .
.
A Cauchy problem is called correctly set if the solution  is uniquely determined by the initial datum
is uniquely determined by the initial datum 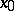 . It is called well-posed (properly posed) if, in addition, the solution
. It is called well-posed (properly posed) if, in addition, the solution  depends continuously on the initial datum
depends continuously on the initial datum 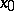 , i.e., for every
, i.e., for every 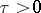 there exists some constant
there exists some constant 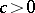 (independent of
(independent of 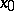 ) such that
) such that
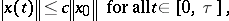 |
and all 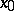 for which a solution exists. Sometimes it is also required that solutions exist for a subspace of initial data which is large enough in an appropriate sense, e.g., dense in
for which a solution exists. Sometimes it is also required that solutions exist for a subspace of initial data which is large enough in an appropriate sense, e.g., dense in 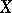 .
.
The notion of a Cauchy problem can be extended to non-autonomous evolution equations [a2], [a5] and to semi-linear [a5], quasi-linear [a5], or fully non-linear evolution equations [a1], [a4]. In this process it may become necessary to replace classical solutions by more general solution concepts (mild solutions [a1], limit solutions [a4], integral solutions (in the sense of Ph. Bénilan; [a4]) in order to keep the problem meaningful. See [a1] and the references therein.
Well-posedness of linear Cauchy problems is intimately linked to the existence of 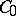 -semi-groups of linear operators (cf. also Semi-group of operators), strongly continuous evolution families [a2], [a5] and related more general concepts like distribution semi-groups, integrated semi-groups, convoluted semi-groups, and regularized semi-groups, while the well-posedness of non-linear Cauchy problems is linked to the existence of non-linear semi-groups (the Crandall–Liggett theorem and its extensions) or (semi-) dynamical systems [a1], [a4], and to (evolutionary) processes and skew product flows [a3].
-semi-groups of linear operators (cf. also Semi-group of operators), strongly continuous evolution families [a2], [a5] and related more general concepts like distribution semi-groups, integrated semi-groups, convoluted semi-groups, and regularized semi-groups, while the well-posedness of non-linear Cauchy problems is linked to the existence of non-linear semi-groups (the Crandall–Liggett theorem and its extensions) or (semi-) dynamical systems [a1], [a4], and to (evolutionary) processes and skew product flows [a3].
References
| [a1] | P. Benilan, P. Wittbold, "Nonlinear evolution equations in Banach spaces: Basic results and open problems" K.D. Bierstedt (ed.) A. Pietsch (ed.) W.M. Ruess (ed.) D. Vogt (ed.) , Functional Analysis , Lecture Notes Pure Appl. Math. , 150 , M. Dekker (1994) pp. 1–32 |
| [a2] | H.O. Fattorini, "The Cauchy problem" , Addison-Wesley (1983) |
| [a3] | J.K. Hale, "Asymptotic behavior of dissipative systems" , Amer. Math. Soc. (1988) |
| [a4] | V. Lakshmikantham, S. Leela, "Nonlinear differential equations in abstract spaces" , Pergamon (1981) |
| [a5] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
Abstract Cauchy problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_Cauchy_problem&oldid=17701