Abel transformation
summation by parts
A transformation
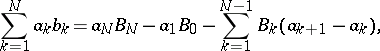 |
where 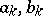 are given,
are given, 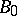 is arbitrarily selected, and
is arbitrarily selected, and
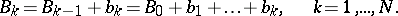 |
The Abel transformation is the discrete analogue of the formula for integration by parts.
If  and if the sequence
and if the sequence 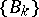 is bounded, then the Abel transformation can be applied to the series
is bounded, then the Abel transformation can be applied to the series
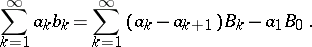 |
The Abel transformation is used to prove several criteria of convergence of series of numbers and functions (cf. Abel criterion). The Abel transformation of a series often yields a series with an identical sum, but with a better convergence. It is also regularly used to obtain certain estimates (cf. Abel inequality), in particular, for investigations on the rate of convergence of a series. It was introduced by N.H. Abel [1].
References
| [1] | N.H. Abel, "Untersuchungen über die Reihe 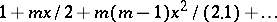 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , 1–2 , Cambridge Univ. Press (1952) |
Abel transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_transformation&oldid=13523