Abel summation method

One of the methods for the summation of series of numbers. The series

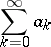can be summed by the Abel method (-method) to the number if, for any real , , the series

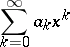is convergent and

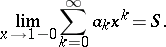This summation method can already be found in the works of L. Euler and G. Leibniz. The name "Abel summation method" originates from the Abel theorem on the continuity of power series. The Abel summation method belongs to the class of totally regular summation methods and is more powerful than the entire set of Cesàro summation methods. The Abel summation method is used in conjunction with Tauberian theorems to demonstrate the convergence of a series.

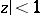A closely related summation method is the -method. Let be a complex number, ; the series

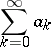is summed by the 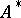-method to the number 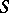if

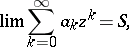where 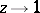along any path not tangent to the unit circle.

References

[1]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)
[2]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)