Artin root numbers
A global Artin root number is a complex number $W ( \rho )$ of modulus $1$ appearing in the functional equation of an Artin $L$-series (cf. also $L$-function)
\begin{equation} \tag{a1} \Lambda ( s , \rho ) = W ( \rho ) . \Lambda ( 1 - s , \overline { \rho } ), \end{equation}
in which $\rho$ is a representation
\begin{equation*} \rho : \operatorname { Gal } ( N / K ) \rightarrow G l _ { n } ( C ) \end{equation*}
of the Galois group of a finite Galois extension $N / K$ of global fields (cf. also Representation theory; Galois theory; Extension of a field), $\rho$ denotes the complex-conjugate representation, and $\Lambda ( s , \rho )$ is the (extended) Artin $L$-series with gamma factors at the Archimedean places of $K$ (details can be found in [a6]).
Work of R. Langlands (unpublished) and P. Deligne [a2] shows that the global Artin root number can be written canonically as a product
\begin{equation*} W ( \rho ) = \prod W _ { P } ( \rho ) \end{equation*}
of other complex numbers of modulus $1$, called local Artin root numbers (Deligne calls them simply "local constants" ). Given $\rho$, there is one local root number $W _ { P } ( \rho )$ for each non-trivial place $P$ of the base field $K$, and $W _ { P } ( \rho ) = 1$ for almost all $P$.
Interest in root numbers arises in part because they are analogues of Langlands'  -factors appearing in the functional equations of $L$-series associated to automorphic forms. In special settings, global root numbers are known to have deep connections to the vanishing of Dedekind zeta-functions at $s = 1 / 2$ (cf. also Dedekind zeta-function), and to the existence of a global normal integral basis, while local root numbers are connected to Stiefel–Whitney classes, to Hasse symbols of trace forms, and to the existence of a canonical quadratic refinement of the local Hilbert symbol. Excellent references containing both a general account as well as details can be found in [a6], [a11] and [a4].
-factors appearing in the functional equations of $L$-series associated to automorphic forms. In special settings, global root numbers are known to have deep connections to the vanishing of Dedekind zeta-functions at $s = 1 / 2$ (cf. also Dedekind zeta-function), and to the existence of a global normal integral basis, while local root numbers are connected to Stiefel–Whitney classes, to Hasse symbols of trace forms, and to the existence of a canonical quadratic refinement of the local Hilbert symbol. Excellent references containing both a general account as well as details can be found in [a6], [a11] and [a4].
Some observations.
a) The global and the local root numbers of $\rho$ depend only on the isomorphism class of $\rho$; hence the root numbers are functions of the character $\chi = \text { trace o } \rho$.
b) When the character of $\rho$ is real-valued, then the global root number $W ( \rho )$ has value $\pm 1$, and each local root number is a fourth root of unity.
c) [a1] When $\operatorname{Gal}( N / K )$ has a representation $\rho$ whose character is real-valued and whose global root number $W ( \rho )$ is $- 1$, then the Dedekind zeta-function $\zeta_N ( s )$ vanishes at $s = 1 / 2$.
d) [a5] When $\rho$ is a real representation (a condition stronger than the requirement that the character be real-valued), then the global root number $W ( \rho )$ is $+ 1$. This means that the product of the local root numbers of a real representation is $+ 1$, so the Fröhlich–Queyrut theorem is a reciprocity law (cf. Reciprocity laws), or a "product formula" , for local root numbers. Some authors write "real orthogonal" or just "orthogonal" in place of "real representation" ; all three concepts are equivalent.
e) [a12] A normal extension of number fields $N / K$ has a normal integral basis if and only if $N / K$ is at most tamely ramified and the global root number $W ( \rho ) = 1$ for all irreducible symplectic representations $\rho$ of $\operatorname{Gal}( N / K )$. (By definition, the extension has a normal integral basis provided the ring of integers $O _ { \text{N} }$ is a free $\mathbf{Z}[ \text{Gal} (N/K)]$-module).
f) [a3] Let $\rho$ be a real representation and let $\operatorname{det}_ { \rho }$ be the $1$-dimensional real representation obtained by composing $\rho$ with the determinant. Then for each place $P$ of $K$, the normalized local Artin root number $W _ { P } ( \rho ) / W _ { P } ( \operatorname { det } _ { \rho } )$ equals the second Stiefel–Whitney class $w _ { 2 } ( \rho _ { P } )$ of the restriction of $\rho$ to a decomposition subgroup of $P$ in $\operatorname{Gal}( N / K )$.
g) [a9] Let $E / K$ be a finite extension of number fields, with normal closure $N / K$. Let $\rho$ be the representation of $\operatorname{Gal}( N / K )$ induced by the trivial representation of $\operatorname { Gal } ( N / E )$. Then the Hasse symbol $h _ { P }$ at $P$ of the trace form $\operatorname {trace}_{E/K} ( x ^ { 2 } )$ is given by $h _ { p } = ( 2 , d ) _ { P } \cdot W _ { P } ( \rho ) / W _ { P } ( \operatorname { det } _ { \rho } )$, where $d$ is the discriminant of the trace form and $( 2 , d ) _ { P }$ is a Hilbert symbol (cf. Norm-residue symbol).
h) [a11] For a place $P$ and a non-zero element $a \in K ^ { * }$, the $1$-dimensional real representation $\rho _ { a }$ sending $g \in G$ to $\rho _ { a } ( g ) = g ( \sqrt { a } ) / \sqrt { a }$ has a local root number $W _ { P } (\, \rho _ { a } )$, which will be abbreviated by $r _ { P } ( a )$. For $P$ fixed, these local root numbers produce a mapping
\begin{equation*} r _ { P } : K _ { P } ^ { * } / K _ { P } ^ { * 2 } \rightarrow C ^ { * } \end{equation*}
which satisfies
\begin{equation} \tag{a2} r _ { P } ( a \cdot b ) = r _ { P } ( a ) \cdot r _ { P } ( b ) \cdot ( a , b ) _ { P }. \end{equation}
The last factor is the local Hilbert symbol at $P$; it gives a non-degenerate inner product on the local square class group at $P$, viewed as a vector space over the field of two elements, the latter identified with $\{ \pm 1 \}$. Equation (a2) has been interpreted in [a7] to mean that the local root numbers give a canonical "quadratic refinement" of this inner product.
Remarks.
1) It follows formally from (a1) that $W ( \rho ) \cdot W ( \overline { \rho } ) = 1$. Moreover, $W ( \overline { \rho } ) = \overline { W ( \rho ) }$, so the global root number $W ( \rho )$ has modulus $1$. When the character of $\rho$ is real-valued, then $\rho$ and $\rho$ are isomorphic, so their global root numbers are equal: $W ( \rho ) = W ( \overline { \rho } )$. It follows that the global root number $W ( \rho ) = \pm 1$.
2) Statement c) follows from the basic argument in [a1], Sect. 3, with minor modifications.
3) To put Taylor's theorem in context, let $N / K$ be a finite Galois extension of fields, with Galois group $G$. Then the normal basis theorem of field theory says that $N$ has a $K$-basis consisting of the Galois conjugates of a single element; restated, $N$ is a free $K [ G ]$-module. When $N / K$ is an extension of number fields, one can ask for a normal integral basis. There are two different notions: One can require the ring of integers $O _ { \text{N} }$ to be a free $O _ { K } [G]$ module (necessarily of rank $1$), or one can require $O _ { \text{N} }$ to be a free $\mathbf Z [ G ]$-module (necessarily of rank $[ K : Q ]$). These notions coincide when the base field $K$ is the field of rational numbers. At present (1998), little is known about the first notion, so the second is chosen. Thus, $N / K$ has a normal integral basis when $O _ { \text{N} }$ has a $\mathbf{Z}$-basis $\{ a _ { j } ^ { g } : j = 1 , \dots , [ K : Q ] , g \in G \}$. By results of E. Noether and R. Swan (see [a4], pp. 26–28), a necessary condition for $N / K$ to have a normal integral basis is that $N / K$ be at most tamely ramified. A. Fröhlich conjectured and M. Taylor proved that the extra conditions beyond tameness needed to make $O _ { \text{N} }$ a free $\mathbf Z [ G ]$-module is for all the global root numbers of symplectic representations to have value $1$.
To say that a complex representation $\rho$ is symplectic means that the representation has even dimension, $2 n$, and factors through the symplectic group $\rho : G \rightarrow S p _ { 2 n } ( C ) \rightarrow G l _ { 2 n } ( C )$. The character values of a symplectic representation are real. A useful criterion is: When $\rho$ is irreducible with character 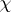 , then the sum
, then the sum
\begin{equation*} | G | ^ { - 1 } \sum _ { g \in G } \chi ( g ^ { 2 } ) \end{equation*}
takes the value $- 1$ when $\rho$ is symplectic, the value $1$ when $\rho$ is real, and the value $0$ in all other cases (see [a10], Prop. 39).
4) The families of complex numbers which can be realized as the local root numbers of some real representation of the Galois group of some normal extension $N / Q$ have been determined in [a8].
References
| [a1] | J.V. Armitage, "Zeta functions with zero at $s = 1 / 2$" Invent. Math. , 15 (1972) pp. 199–205 |
| [a2] | P. Deligne, "Les constantes des équation fonctionelles des fonctions $L$" , Lecture Notes Math. , 349 , Springer (1974) pp. 501–597 |
| [a3] | P. Deligne, "Les constantes locales de l'équation fonctionelle des fonction $L$ d'Artin d'une répresentation orthogonale" Invent. Math. , 35 (1976) pp. 299–316 |
| [a4] | A. Fröhlich, "Galois module structure of algebraic integers" , Ergebn. Math. , 1 , Springer (1983) |
| [a5] | A. Fröhlich, J. Queyrut, "On the functional equation of the Artin L-function for characters of real representations" Invent. Math. , 20 (1973) pp. 125–138 |
| [a6] | J. Martinet, "Character theory and Artin L-functions" , Algebraic Number Fields: Proc. Durham Symp. 1975 , Acad. Press (1977) pp. 1–87 |
| [a7] | R. Perlis, "Arf equivalence I" , Number Theory in Progress: Proc. Internat. Conf. in Honor of A. Schinzel (Zakopane, Poland, June 30--July 9, 1997) , W. de Gruyter (1999) |
| [a8] | R. Perlis, "On the analytic determination of the trace form" Canad. Math. Bull. , 28 : 4 (1985) pp. 422–430 |
| [a9] | J-P. Serre, "L'invariant de Witt de la forme $\operatorname { Tr } ( x ^ { 2 } )$" Comment. Math. Helvetici , 59 (1984) pp. 651–676 |
| [a10] | J-P. Serre, "Représentations linéaires des groupes finis" , Hermann (1971) (Edition: Second) |
| [a11] | J. Tate, "Local constants" , Algebraic Number Fields: Proc. Durham Symp. 1975 , Acad. Press (1977) pp. 89–131 |
| [a12] | M. Taylor, "On Fröhlich's conjecture for rings of integers of tame extensions" Invent. Math. , 63 (1981) pp. 41–79 |
Artin root numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin_root_numbers&oldid=50833