Fuzzy topology

lattice-valued topology, point-set lattice-theoretic topology, poslat topology

A branch of mathematics encompassing any sort of topology using lattice-valued subsets. The following description is based on the standardization of this discipline undertaken in [a9], especially [a10], [a11]; much additional information is given in the references below.

Let $X$ be a set and $( L , \leq , \otimes )$ any complete quasi-monoidal lattice (a cqml; i.e., $( L , \leq )$ is a complete lattice with bottom element $\perp$ and top element $\top$, and the tensor product $\otimes : L \times L \rightarrow L$ is isotone in both arguments with $\top \otimes \top = \top $). Examples of complete quasi-monoidal lattices are:

complete lattices with $\otimes = \wedge$ (binary meet);

$L = [ 0,1 ]$ with $\otimes$ any of the $t$-norms $T _ { \operatorname { min } } ( a , b ) = a \wedge b$, $T _ { \text { prod } } ( a , b ) = a \cdot b$, or $T _ { m } ( a , b ) = ( a + b - 1 ) \vee 0$; or

$L = [ 0,1 ] \times [ 0,1 ]$ with $\otimes$ any of $T_{\text{min}} \times T_{\text{prod}}$, $T _ { \operatorname{prod} } \times T _ { m }$, etc.

$L$-subsets of $X$ comprise the $L$-powerset $L ^ { X } = \{ a : X \rightarrow L , a \ \text {a function } \}$, a complete quasi-monoidal lattice via the lifting of the structure of $L$. A subfamily $\tau \subset L ^ { X }$ is an $L$-topology on $X$, and $( X , \tau )$ is an $L$-topological space, if $\tau$ is closed under $\otimes$ and arbitrary $\vee$ and contains the constant mapping $\underline{ \top } $. A function ${\cal T} : L ^ { X } \rightarrow L$ is an $L$-fuzzy topology on $X$, and $( X , \mathcal{T} )$ is an $L$-fuzzy topological space, if $\mathcal{T}$ satisfies (reading $\forall$ as "for each" ):

1) $\forall$ set $J$, $\forall \{ u_j : j \in J \} \subset L ^ { X }$,

\begin{equation*} \bigwedge _ { j \in J } {\cal T} ( u _ { j } ) \leq {\cal T} \left( \underset { j \in J } { \vee } u _ { j } \right). \end{equation*}

2) $\forall$ two-element set $J$, $\forall \{ u_j : j \in J \} \subset L ^ { X }$,

\begin{equation*} \bigotimes _ { j \in J } \mathcal{T} ( u _ { j } ) \leq \mathcal{T} \left( \bigotimes _ { j \in J } u _ { j } \right) . \end{equation*}

3) $\mathcal{T} ( \underline { \top } ) = \top $.

The member $\mathcal{T} ( u )$ of $L$ is interpreted as the "degree of openness" of $u$.

Important examples of $L$-topological and $L$-fuzzy topological spaces can be found in [a5], Chap. 11; [a6], Kubiak's paper; [a8]; [a9], Chaps. 6, 8, 10; [a9], Chap. 7, Sect. 2.15–2.16; [a10], Sect. 7; [a11], Sect. 7.

For a complete quasi-monoidal lattice $L$ and function $f : X \rightarrow Y$, one defines the powerset operators $f _ { L } ^ { \rightarrow } : L ^ { X } \rightarrow L ^ { Y }$ (the image operator) and $f _ { L } ^ { \leftarrow } : L ^ { Y } \rightarrow L ^ { X }$ (the pre-image operator) by

\begin{equation*} f _ { L } ^ { \rightarrow } ( a ) ( y ) = \vee \{ a ( x ) : f ( x ) = y \}, \end{equation*}

\begin{equation*} f _ { L } ^ { \leftarrow } ( b ) = b \circ f. \end{equation*}

It is well-known that $f _ { L } ^ {\rightarrow} \dashv f _ { L } ^ { \leftarrow }$ and that these operators generalize the traditional operators $f^\rightarrow$ and $f ^ { \leftarrow }$. Given $L$-topological spaces $( X , \tau )$ and $( Y , \sigma )$, a mapping $f : X \rightarrow Y$ is $L$-continuous from $( X , \tau )$ to $( Y , \sigma )$ if $f | _ { \sigma } ^ { \leftarrow } : \tau \leftarrow \sigma$; and given $L$-fuzzy topological spaces $( X , \mathcal{T} )$ and $( Y , \mathcal{S} )$, a mapping $f : X \rightarrow Y$ is $L$-fuzzy continuous from $( X , \mathcal{T} )$ to $( Y , \mathcal{S} )$ if ${\cal T} \circ f ^ { \leftarrow } \geq \cal S$ on $L ^ { Y }$. The category $L$-$\mathbf{TOP}$ comprises $L$-topological spaces, $L$-continuous mappings, and the composition and identities from the category 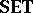(cf. also Sets, category of); and the category $L$-$\textbf{FTOP}$ comprises $L$-fuzzy topological spaces, $L$-fuzzy continuous mappings, and the composition and identities from the category 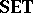. It is a theorem that for all complete quasi-monoidal lattices $L$, the categories $L$-$\mathbf{TOP}$ and $L$-$\textbf{FTOP}$ are topological categories over 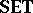, in the sense of [a3] and [a11], Sect. 1, and hence topological constructs.

The above briefly describes "fixed-basis topology" — topology where the complete quasi-monoidal lattice $L$, viewed as the lattice-theoretic base of powersets $L ^ { X }$ and spaces $( X , \tau )$ or $( X , \mathcal{T} )$, is fixed relative to the spaces and mappings of the category $L$-$\mathbf{TOP}$ or $L$-$\textbf{FTOP}$. "Variable-basis topology" permits the base to change within a category, so that each space has its own lattice-theoretic base.

To outline variable-basis topology, note that all complete quasi-monoidal lattices form a category, 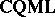, in which morphisms are mappings preserving $\otimes$, arbitrary $\vee$, and $\top$; and also note that $\mathbf{FRM}$ and $\textbf{SFRM}$ embed into 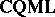. One then considers 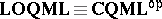, with objects the same as those of 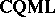, now called localic quasi-monoidal lattices, but morphisms reversed from those of 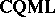; and one notes that $\mathbf{LOC}$ and 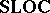embed into .

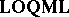Now, let 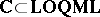. The category $\mathbf{C}$-$\mathbf{TOP}$ for variable-basis topology and the category $\mathbf{C}$-$\textbf{FTOP}$ for variable-basis fuzzy topology are both "concrete" categories over 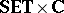as a "ground" or "base" category. For a 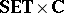morphism $( f , \phi ) : ( X , L ) \rightarrow ( Y , M )$, the pre-image operator $( f , \phi ) ^ { \leftarrow } : L ^ { X } \leftarrow M ^ { Y }$ is defined by $( f , \phi ) ^ { \leftarrow } ( b ) = \phi ^ { \text{op} } \circ b \circ f$. An image operator $( f , \phi ) ^ { \rightarrow }$ is also available which, if $\phi ^ { \operatorname{op} }$ preserves arbitrary $\wedge$, satisfies $( f , \phi )^{ \rightarrow} \dashv ( f , \phi )^{ \leftarrow}$; and if $L = M , \phi ^ { \operatorname{op} } = \operatorname{id} _ { L }$, these operators reduce to their fixed-basis counterparts.

Data for the category $\mathbf{C}$-$\mathbf{TOP}$ include:

objects are topological spaces $( X , L , \tau )$ (cf. also Topological space), where $( X , L ) \in | \mathbf{SET} \times \mathbf{C}|$ and $( X , \tau ) \in | L \square \mathbf{TOP} |$;

morphisms are continuous mappings

\begin{equation*} ( f , \phi ) : ( X , L , \tau ) \rightarrow ( Y , M , \sigma ) \end{equation*}

(cf. also Continuous function), where $( f , \phi ) : ( X , L ) \rightarrow ( Y , M )$ is in 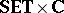and $( f , \phi ) ^ { \leftarrow } | _ { \sigma } : \tau \leftarrow \sigma$.

Data for the category $\mathbf{C}$-$\textbf{FTOP}$ include:

objects are fuzzy topological spaces $( X , L , \mathcal{T} )$, where $( X , L ) \in | \mathbf{SET} \times \mathbf{C}|$ and $( X , \mathcal{T} ) \in | L \square \mathbf{FTOP}|$;

morphisms are fuzzy continuous mappings $( f , \phi ) : ( X , L , \mathcal{T} ) \rightarrow ( Y , M , \mathcal{S} )$, where $( f , \phi ) : ( X , L ) \rightarrow ( Y , M )$ is in 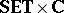and $\mathcal{T} \circ ( f , \phi ) ^ { \leftarrow } \geq \phi ^ { \operatorname{op} } \circ \mathcal{S}$ on $M ^ { Y }$.

In both categories, compositions and identities are those of .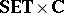

It is a theorem that for all 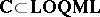, $\mathbf{C}$-$\mathbf{TOP}$ and $\mathbf{C}$-$\textbf{FTOP}$ are topological over the ground 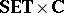in the sense of [a3] and [a11], Sect. 1. Further, these frameworks unify all the fixed-basis categories for topology given above and hence unify all important examples (referenced above) over different lattice-theoretic bases (e.g. two fuzzy real lines $\mathbf{R} ( L )$ and $\mathbf{R} ( M )$). Moreover, all purely lattice-theoretic or point-free approaches to topology — locales, topological molecular lattices, uniform lattices, etc. (see [a1], [a2], [a8]) — categorically embed into $\mathbf{C}$-$\mathbf{TOP}$ or $\mathbf{C}$-$\textbf{FTOP}$ (for appropriate $\mathbf{C}$) as subcategories of singleton spaces; e.g. $\mathbf{LOC}$ embeds as singleton spaces into $\mathbf{LOC}$-$\mathbf{TOP}$. Thus, the variable-basis approach categorically unifies topology and fuzzy topology as a discipline.

References

[a1]	P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1982)
[a2]	G.-J. Wang, "Theory of L-fuzzy topological spaces" , Shanxi Normal Univ. Publ. House (1988) (In Chinese)
[a3]	J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley (1990)
[a4]	U. (ed.) Höhle, "Mathematical aspects of fuzzy set theory" Fuzzy Sets and Syst. , 40 : 2 (1991) (Special Memorial Volume–Second Issue)
[a5]	"Applications of category theory to fuzzy subsets" S.E. Rodabaugh (ed.) E.P. Klement (ed.) U. Höhle (ed.) , Kluwer Acad. Publ. (1992)
[a6]	U. Höhle, S.E. Rodabaugh, A. (eds.) Šostak, "Special issue on fuzzy topology" Fuzzy Sets and Syst. , 73 : 1 (1995)
[a7]	W. (ed.) Kotzé, "Special issue" Quaestiones Math. , 20 : 3 (1997)
[a8]	Liu Ying–Ming, Luo Mao–Kang, "Fuzzy topology" , World Sci. (1997)
[a9]	"Mathematics of fuzzy sets: Logic, topology, and measure theory" U. Höhle (ed.) S.E. Rodabaugh (ed.) , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999)
[a10]	U. Höhle, A. Šostak, "Axiomatic foundations of fixed-basis fuzzy topology" U. Höhle (ed.) S.E. Rodabaugh (ed.) , Mathematics of Fuzzy Sets: Logic, Topology, and Measure Theory , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999) pp. 123–272
[a11]	S.E. Rodabaugh, "Categorical foundations of variable-basis fuzzy topology" U. Höhle (ed.) S.E. Rodabaugh (ed.) , Mathematics of Fuzzy Sets: Logic, Topology, and Measure Theory , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999) pp. 273–388