Wiener sausage
Let $\beta ( t )$, $t \geq 0$, be the standard Brownian motion in $\mathbf{R} ^ { d }$ (i.e. the Markov process with generator $\Delta / 2$) starting at $0$. Let $\textsf{P}$, $\mathsf{E}$ denote its probability law and expectation on path space. The Wiener sausage with radius $a > 0$ is the process defined by
\begin{equation*} W ^ { a } ( t ) = \bigcup _ { 0 \leq s \leq t } B _ { a } ( \beta ( s ) ) , \quad t \geq 0, \end{equation*}
where $B _ { a } ( x )$ is the open ball with radius $a$ around $x \in \mathbf{R} ^ { d }$.
The Wiener sausage is an important mathematical object, because it is one of the simplest examples of a non-Markovian functional of Brownian motion. It plays a key role in the study of various stochastic phenomena, such as heat conduction and trapping in random media, as well as in the analysis of spectral properties of random Schrödinger operators (cf. also Schrödinger equation).
A lot is known about the behaviour of the volume of $W ^ { a } ( t )$ as $t \rightarrow \infty$. For instance,
\begin{equation*} \mathsf{E} | W ^ { a } ( t ) | \sim \left\{ \begin{array} { l l } { \sqrt { \frac { 8 t } { \pi } } , } & { d = 1, } \\ { \frac { 2 \pi t } { \operatorname { log } t } , } & { d = 2, } \\ { \kappa _ { a } t , } & { d \geq 3, } \end{array} \right. \end{equation*}
with $\kappa _ { a } = a ^ { d - 2 } 2 \pi ^ { d / 2 } / \Gamma ( ( d - 2 ) / 2 )$ the Newtonian capacity of $B _ { a } ( 0 )$ associated with the Green's function of $( - \Delta / 2 ) ^ { - 1 }$ (cf. also Green function; Capacity), and
\begin{equation*} \operatorname { Var } | W ^ { a } ( t ) | \asymp \left\{ \begin{array} { l l } { t , } & { d = 1, } \\ { \frac { t ^ { 2 } } { \operatorname { log } ^ { 4 } t } , } & { d = 2, } \\ { \operatorname { tlog } t , } & { d = 3, } \\ { t , } & { d \geq 4 } \end{array} \right. \end{equation*}
([a8], [a6]). Moreover, $| W^ { a } ( t ) |$ satisfies the strong law of large numbers and the central limit theorem for $d \geq 2$; the limit law is Gaussian for $d \geq 3$ and non-Gaussian for $d = 2$ ([a7]). Note that for $d \geq 2$ the Wiener sausage is a sparse object: since the Brownian motion typically travels a distance $\sqrt { t }$ in each direction, the last two displays show that most of the space in the convex hull of $W ^ { a } ( t )$ is not covered.
The large deviation behaviour of $| W^ { a } ( t ) |$ in the downward direction has been studied in [a5], [a4] and [a9]. For $d \geq 2$ the outcome, proved in successive stages of refinement, reads as follows:
\begin{equation*} \operatorname { lim } _ { t \rightarrow \infty } \frac { f ( t ) ^ { 2 / d } } { t } \operatorname { log } \mathsf{P} ( | W ^ { a } ( t ) | \leq f ( t ) ) = - \frac { 1 } { 2 } \lambda _ { d } \end{equation*}
for any $f : \mathbf{R} _ { + } \rightarrow \mathbf{R} _ { + }$ satisfying $\operatorname { lim } _ { t \rightarrow \infty } f ( t ) = \infty$ and
\begin{equation*} f ( t ) = \left\{ \begin{array} { l l } { o \left( \frac { t } { \operatorname { log } t } \right) , } & { d = 2, } \\ { o ( t ) , } & { d \geq 3, } \end{array} \right. \end{equation*}
where $\lambda _ { d } > 0$ is the smallest Dirichlet eigenvalue of $- \Delta$ on the ball with unit volume. The optimal strategy for the Brownian motion to realize the large deviation is to stay inside a ball with volume $f ( t )$ until time $t$, i.e., the Wiener sausage covers this ball entirely and nothing outside. This comes from the Faber–Krahn isoperimetric inequality (cf. also Rayleigh–Faber–Krahn inequality), and the cost of staying inside the ball is
\begin{equation*} \operatorname { exp } \left[ - \frac { 1 } { 2 } \lambda _ { d } \frac { t } { f ( t ) ^ { 2 / d } } \right] \end{equation*}
to leading order. Note that, apparently, a large deviation below the scale of the mean "squeezes all the empty space out of the Wiener sausage" .
The above analysis of the large deviation behaviour has recently been extended to cover the moderate deviation behaviour. It is proved in [a2] that for $d \geq 3$,
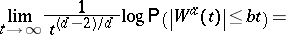 | (a1) |
\begin{equation*} = - I ^ { \kappa_a } ( b ) \in ( - \infty , 0 ) , \text { for all } 0 < b < \kappa _ { a }, \end{equation*}
and a variational representation is derived for the rate function 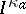 . The optimal strategy for the Brownian motion to realize the moderate deviation is such that the Wiener sausage "looks like a Swiss cheese" : $W ^ { a } ( t )$ has random holes whose sizes are of order $1$ and whose density varies on scale $t ^ { 1 / d }$. This is markedly different from the optimal strategy behind the large deviation. Note that, apparently, a moderate deviation on the scale of the mean "does not squeeze all the empty space out of the Wiener sausage" . (a1) has also been extended to $d = 2$.
. The optimal strategy for the Brownian motion to realize the moderate deviation is such that the Wiener sausage "looks like a Swiss cheese" : $W ^ { a } ( t )$ has random holes whose sizes are of order $1$ and whose density varies on scale $t ^ { 1 / d }$. This is markedly different from the optimal strategy behind the large deviation. Note that, apparently, a moderate deviation on the scale of the mean "does not squeeze all the empty space out of the Wiener sausage" . (a1) has also been extended to $d = 2$.
It turns out that the rate function $b \mapsto I ^ { \kappa_a } ( b )$ exhibits rich behaviour as a function of the dimension. In particular, for $d \geq 5$ it is non-analytic at a certain critical value inside $( 0 , \kappa _ { a} )$, which is associated with a collapse transition in the optimal strategy.
Finally, the moderate and large deviations of $| W^ { a } ( t ) |$ in the upward direction are a complicated issue. Here the optimal strategy is entirely different from the previous ones, because the Wiener sausage tries to expand rather than to contract. Partial results have been obtained in [a3] [a1], and [a11].
More background can be found in [a10].
References
| [a1] | M. van den Berg, E. Bolthausen, "Asymptotics of the generating function for the volume of the Wiener sausage" Probab. Th. Rel. Fields , 99 (1994) pp. 389–397 |
| [a2] | M. van den Berg, E. Bolthausen, F. den Hollander, "Moderate deviations for the volume of the Wiener sausage" Ann. of Math. (to appear in 2001) |
| [a3] | M. van den Berg, B. Tóth, "Exponential estimates for the Wiener sausage" Probab. Th. Rel. Fields , 88 (1991) pp. 249–259 |
| [a4] | E. Bolthausen, "On the volume of the Wiener sausage" Ann. Probab. , 18 (1990) pp. 1576–1582 |
| [a5] | M.D. Donsker, S.R.S. Varadhan, "Asymptotics for the Wiener sausage" Commun. Pure Appl. Math. , 28 (1975) pp. 525–565 |
| [a6] | J.-F. Le Gall, "Sur une conjecture de M. Kac" Probab. Th. Rel. Fields , 78 (1988) pp. 389–402 |
| [a7] | J.-F. Le Gall, "Fluctuation results for the Wiener sausage" Ann. Probab. , 16 (1988) pp. 991–1018 |
| [a8] | F. Spitzer, "Electrostatic capacity, heat flow and Brownian motion" Z. Wahrsch. Verw. Gebiete , 3 (1964) pp. 110–121 |
| [a9] | A.-S. Sznitman, "Long time asymptotics for the shrinking Wiener sausage" Commun. Pure Appl. Math. , 43 (1990) pp. 809–820 |
| [a10] | A.-S. Sznitman, "Brownian motion, obstacles and random media" , Springer (1998) |
| [a11] | Y. Hamana, H. Kesten, "A large deviation result for the range of random walk and for the Wiener sausage" preprint March (2000) |
Wiener sausage. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_sausage&oldid=50072