BGG resolution
The structure of a real Lie group $G$ can be studied by considering representations of the complexification $\frak g$ of its Lie algebra (cf. also Representation of a Lie algebra). These are viewed as left modules over the universal enveloping algebra $U ( \mathfrak { g } )$ of $\frak g$, or $\frak g$-modules. The Lie algebras $\frak g$ considered here are the complexifications of real semi-simple Lie algebras corresponding to real, connected, semi-simple Lie groups. A Cartan subalgebra $\mathfrak h $, that is, a maximal Abelian subalgebra with the property that its adjoint representation on $\frak g$ is semi-simple, is chosen (cf. also Cartan subalgebra). A root system $\Delta \subset \mathfrak { h } ^ { * }$, corresponding to the resulting decomposition of $\frak g$, is obtained. A further choice of a positive root system $\Delta ^ { + } \subset \Delta$ determines subalgebras $\mathfrak n$ and $\mathfrak{n}^{-}$ corresponding to the positive and negative root spaces, respectively. The building blocks in the study of $G$ are the finite-dimensional irreducible $\frak g$-modules $L ( \lambda )$. They are indexed by the set $P ^ { + } \subset \mathfrak { h } ^ { * }$ of dominant integral weights $\lambda$ relative to $\Delta ^ { + }$.
For any ring $A$ with unity, a resolution of a left $A$-module $M$ is an exact chain complex of $A$-modules:
\begin{equation*} \ldots \rightarrow D _ { 2 } \stackrel { \delta _ { 2 } } { \rightarrow } D _ { 1 } \stackrel { \delta _ { 1 } } { \rightarrow } D _ { 0 } \stackrel { \delta _ { 0 } } { \rightarrow } M \rightarrow 0. \end{equation*}
For example, let $\frak a$ be a complex Lie algebra, and let $D _ { k } = U ( \mathfrak{a} ) \otimes _ { \mathbf{C} } \wedge ^ { k } ( \mathfrak{a} )$, where $\wedge ^ { k } (\mathfrak{a} )$ is the $k$th exterior power of $\frak a$, $k = 0 , \ldots , n = \operatorname { dim } \mathfrak{a}$. Let
\begin{equation*} \delta _ { k } ( X \bigotimes X _ { 1 } \bigwedge \ldots \bigwedge X _ { k } ) = \end{equation*}
\begin{equation*} = \sum _ { i = 1 } ^ { k } ( - 1 ) ^ { i + 1 } X X _ { i } \bigotimes X _ { 1 } \bigwedge \ldots \bigwedge \hat{X} _ { i } \bigwedge \ldots \bigwedge X _ { k } + \end{equation*}
\begin{equation*} + \sum _ { 1 \leq i < j \leq k } ( - 1 ) ^ { i + j } X \bigotimes [ X , X _ { j } ] \bigwedge \end{equation*}
 |
where $X \in U ( \mathfrak{a} )$, $X _ { i } \in \mathfrak{a}$ and $\hat{X}_i$ means that $X_i$ has been omitted. Let $\delta _ { 0 } ( X )$ be the constant term of $X \in U ( \mathfrak{a} )$. Then
\begin{equation*} 0 \rightarrow D _ { n } \stackrel { \delta _ { n } } { \rightarrow } \ldots \stackrel { \delta _ { 1 } } { \rightarrow } D _ { 0 } \stackrel { \delta _ { 0 } } { \rightarrow } \mathbf{C} \rightarrow 0 \end{equation*}
is the standard resolution $V ( \mathfrak{a} )$ of the trivial $\frak a$-module $\mathbf{C}$. If $\mathfrak{p} \subset \mathfrak{a}$ is a subalgebra, one considers the relative version $V ( \mathfrak{a} , \mathfrak{p} )$ of $V ( \mathfrak{a} )$ by setting $\overline { D } _ { k } = U ( {\frak a} ) \otimes_{U ( {\frak p} )} \wedge ^ { k } ( {\frak a}/ \frak{p} )$. One observes that the obvious modification of the $\delta _ { k }$ produces mappings $\overline { \delta } _{k} : \overline { D } _ { k } \rightarrow \overline { D } _ { k - 1 }$, $k = 1 , \ldots , r = \operatorname { dim } \mathfrak{a} / \mathfrak{p}$, and that the resulting complex is similarly exact.
In [a3] two constructions of a resolution of $L = L ( \lambda )$, $\lambda \in P ^ { + }$, were obtained. They are described below.
Weak BGG resolution.
Let $\mathfrak { b } = \mathfrak { h } \oplus \mathfrak { n } \subset \mathfrak { g }$ and let $\mathcal{O}$ be the category of finitely-generated $\mathfrak h $-diagonalizable $U ( {\frak n} )$-finite $\frak g$-modules ([a2]). Let $Z ( {\frak g} )$ denote the centre of $U ( \mathfrak { g } )$. If M is a $\frak g$-module, let $\Theta( M ) \subset Z ( \mathfrak { g } ) ^ { * }$ denote the set of eigenvalues of $M$. For $\theta \in \Theta ( M )$, let $M _ { \theta }$ denote the eigenspace associated to $\theta$. The set $\Theta( L ( \lambda ) )$ consists of only one element, denoted by $\theta _ { \lambda }$. For $M \in \mathcal{O}$, $\mathfrak { F } _ { \lambda } ( M ) = ( M \otimes L ( \lambda ) ) _ { \theta _ { \lambda } }$ defines an exact functor in $\mathcal{O}$. If $r = \operatorname { dim } \mathfrak{n}^-$, let
\begin{equation*} ( B , \delta ) : 0 \rightarrow B _ { r } \stackrel { \delta _ { r } } { \rightarrow } \ldots \stackrel { \delta _ { 1 } } { \rightarrow } B _ { 1 } \stackrel { \delta _ { 0 } } { \rightarrow } L ( \lambda ) \rightarrow 0 \end{equation*}
be the image of $V ( \mathfrak { g } , \mathfrak { b } )$ under the functor $\mathfrak { F } _ { \lambda }$. $( B , \delta )$ is known as the weak BGG resolution. Its importance lies in the property of the $B _ { k }$ explained below. For $\mu \in \mathfrak { h } ^ { * }$, ${\bf C} ( \mu )$ denotes the trivially extended action of $\mu$ from $\mathfrak h $ to $\mathfrak{b}$. The $\frak g$-module $M ( \mu ) = U ( \mathfrak { g } ) \otimes_{ U ( \mathfrak { b } )} \mathbf{C} ( \mu )$ is the Verma module associated to $\mu$. Let $\Pi \subset \Delta ^ { + }$ denote the set of simple (i.e. indecomposable in $\Delta ^ { + }$, positive roots. Let $W$ be the group of automorphisms of $\mathfrak{h} ^ { * }$ generated by the reflections $\sigma _ { \alpha }$ relative to $\alpha \in \Pi$ (cf. also Weyl group). Let $W ^ { ( i ) }$ be the set of elements $w \in W$ that are minimally expressed as a product of $i$ reflections $\sigma _ { \alpha }$, $\alpha \in \Pi$. One writes $W ^ { ( i ) } = \{ w \in W : l ( w ) = i \}$. Each $B _ { k }$ has a filtration (cf. also Filtered algebra) $B _ { k } = M _ { 1 } \supset \ldots \supset M _ { s } = 0$ of $\frak g$-modules such that $M _ { i } / M _ { i - 1 } \simeq M ( \mu _ { i } )$ and $\{ \mu _ { i } \} _ { i = 1 } ^ { s - 1 } = \{ w \cdot \lambda \} _ { w \in W ^ { ( k ) } }$, where $w.\mu = w ( \mu + \rho ) - \rho$ and $\rho = ( 1 / 2 ) \sum _ { \alpha \in \Delta ^ { + } } \alpha$.
If $\frak a$ is a Lie algebra and
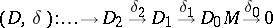 |
is a resolution of the $\frak a$-module $M$ by projective $\frak a$-modules, and $( \operatorname{Hom} _ {\frak a } ( D , N ) , \delta ^ { \prime } )$ is the image of $( D , \delta )$ under the functor $\operatorname { Hom } _ { a }( - , N ) : N ^ { \prime } \rightarrow \operatorname { Hom } _ { a } ( N ^ { \prime } , N )$, then $\operatorname { Ext } _ { a } ^ { i } ( M , N ) = \operatorname { Ker } \delta _ { i + 1 } ^ { \prime } / \operatorname { Im } \delta _ { i } ^ { \prime }$. The cohomology groups $H ^ { i } ( \mathfrak{a} , M )$ are defined as $\operatorname{Ext}_{\mathfrak{a}}^i( \mathbf{C} , M)$. If $L = L ( \lambda )$, and $\lambda \in P ^ { + }$, the weak BGG resolution implies that $\operatorname{dim} H ^ { i } ( \mathfrak { n } ^ { - } , L ) = \# W ^ { ( i ) }$.
Strong BGG resolution.
For $w _ { 1 } , w _ { 2 } \in W$ one writes $w _ { 1 } \leftarrow w _ { 2 }$ if there exists a $\gamma \in \Delta _ { + }$ such that $w _ { 1 } = \sigma _ { \gamma } w _ { 2 }$ and $l ( w _ { 1 } ) = l ( w _ { 2 } ) + 1$. This relation induces a partial ordering $\leq$ on $W$, by setting $w \leq w ^ { \prime }$ whenever there are $w _ { 1 } , \dots , w _ { k }$ in $W$ such that $w = w _ { 1 } \leftarrow \ldots \leftarrow w _ { k } = w ^ { \prime }$. It was shown in [a1] that
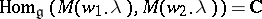 |
if and only if $w _ { 1 } \leq w _ { 2 }$. Furthermore, every such homomorphism is zero or injective. One fixes, for each pair $( w _ { 1 } , w _ { 2 } )$, one such injection $i_{w _ { 1 } , w_ { 2 }}$. Let $C _ { k } = \oplus _ { w \in W ^ { ( i ) } } M ( w . \lambda )$. Therefore, a $\frak g$-homomorphism $d _ { k } : C _ { k } \rightarrow C _ { k - 1 }$ is determined by a complex matrix $( c _ { w _ { 1 } , w _ { 2 }} )$ with $w _ { 1 } \in W ^ { ( k ) }$ and $w _ { 2 } \in W ^ { ( k - 1 ) }$. It is shown in [a3] that there exist $c _{w_{ 1 } , w _ { 2 } } \in \{ \pm 1 \}$, $w _ { 1 } \in W ^ { ( k ) }$, $w _ { 1 } \leftarrow w _ { 2 }$, for $k = 1 , \dots , r = \operatorname { dim } \mathfrak{n} ^ { - }$, such that
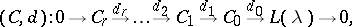 |
where $d _ { 0 } : M ( \lambda ) \rightarrow L ( \lambda )$ is the canonical surjection, is exact. This strong BGG resolution refines the weak BGG resolution $( B , \delta )$ and, in particular, calculates the cohomology groups $H ^ { i } ( \mathfrak { h } ^ { - } , L )$. In [a4] it was proved that the weak and the strong BGG resolutions are isomorphic. The results of [a4] apply to the more general situation of parabolic subalgebras $\mathfrak { p } \supset \mathfrak{b}$. They imply the existence of a complex in terms of the degenerate principal series representations of $G$ that has the same cohomology as the de Rham complex [a4]. The BGG resolution has been extended to Kac–Moody algebras (see [a5] and also Kac–Moody algebra) and to the Lie algebra of vector fields on the circle [a6].
References
| [a1] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "Structure of representations generated by vectors of highest weight" Funkts. Anal. Prilozh. , 5 : 1 (1971) pp. 1–9 |
| [a2] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "A certain category of $\frak g$-modules" Funkts. Anal. Prilozh. , 10 : 2 (1976) pp. 1–8 |
| [a3] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "Differential operators on the base affine space and a study of $\frak g$-modules" I.M. Gelfand (ed.) , Lie groups and their representations, Proc. Summer School on Group Representations , Janos Bolyai Math. Soc.&Wiley (1975) pp. 39–64 |
| [a4] | A. Rocha-Caridi, "Splitting criteria for $\frak g$-modules induced from a parabolic and the Bernstein–Gelfand–Gelfand resolution of a finite dimensional, irreducible $\frak g$-module" Trans. Amer. Math. Soc. , 262 : 2 (1980) pp. 335–366 |
| [a5] | A. Rocha-Caridi, N.R. Wallach, "Projective modules over graded Lie algebras" Math. Z. , 180 (1982) pp. 151–177 |
| [a6] | A. Rocha-Caridi, N.R. Wallach, "Highest weight modules over graded Lie algebras: Resolutions, filtrations and character formulas" Trans. Amer. Math. Soc. , 277 : 1 (1983) pp. 133–162 |
BGG resolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BGG_resolution&oldid=50034