Schur functions in algebraic combinatorics

The Schur functions $s_{ \lambda }$ are a special basis for the algebra of symmetric functions $\Lambda$. They are also intimately connected with representations of the symmetric and general linear groups (cf. also Representation of the symmetric groups). Standard references are [a3], [a6], [a8], [a9].

Definitions.

Let $\mathbf{x} = \{ x _ { 1 } , \dots , x _ { l } \}$ be a set of variables and let $\Lambda$ be the algebra of symmetric functions in $\mathbf{x}$. Bases for this algebra are indexed by partitions $\lambda = ( \lambda _ { 1 } , \dots , \lambda _ { l } )$, i.e., $\lambda$ is a weakly decreasing sequence of $l$ non-negative integers $\lambda _ { i }$ called parts. Associated with any partition is an alternant, which is the $l \times l$ determinant

\begin{equation*} a_\lambda = \operatorname { det } ( x _ { i } ^ { \lambda_j } ). \end{equation*}

In particular, for the partition $\delta = ( l - 1 , l - 2 , \ldots , 0 )$ one has the Vandermonde determinant $a _ { \delta } = \prod _ { i < j } ( x _ { i } - x _ { j } )$. In his thesis [a11], I. Schur defined the functions which bear his name as

\begin{equation*} s _ { \lambda } = \frac { a _ { \lambda + \delta} } { a _ { \delta } }, \end{equation*}

where addition of partitions is component-wise. It is clear from this equation that $s_{ \lambda }$ is a symmetric homogeneous polynomial of degree $| \lambda | = \Sigma _ { i } \lambda_i$.

There is a more combinatorial definition of a Schur function. A partition $\lambda$ can be viewed as a Ferrers shape, obtained by placing dots or cells in $l$ left-justified rows with $\lambda _ { i }$ boxes in row $i$. One obtains a semi-standard Young tableaux, $T$, of shape $\lambda$ by replacing each dot by a positive integer so that rows weakly increase and columns strictly increase (cf. also Young tableau). For example, if $\lambda = ( 4,2,1 )$, then its shape and a possible tableau are

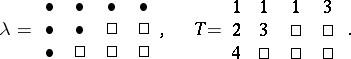Each tableau determines a monomial $x ^ { T } = \prod _ { i \in T } x _ { i }$, e.g., in the example above, $x ^ { T } = x _ { 1 } ^ { 3 } x _ { 2 } x _ { 3 } ^ { 2 } x _ { 4 }$. The second definition of the Schur function is then

\begin{equation*} s _ { \lambda } = \sum _ { T } \mathbf{x} ^ { T }, \end{equation*}

where the sum is over all semi-standard Young tableaux of shape $\lambda$ with entries between $1$ and $l$.

Change of basis.

The Schur functions can also be written in terms of the other standard bases for $\Lambda$. A monomial symmetric function $m _ { \lambda }$ is the sum of all monomials whose exponent sequence is some permutation of $\lambda$. Also, define the Kostka number [a5] $K _ { \lambda \mu }$ as the number of semi-standard Young tableaux $T$ of shape $\lambda$ and content $\mu = ( \mu _ { 1 } , \dots , \mu _ { l } )$, i.e., $T$ contains $\mu _ { i }$ entries equal to $i$ for $1 \leq i \leq l$. The combinatorial definition of $s_{ \lambda }$ immediately gives the following rule, known as Young's rule:

\begin{equation*} s _ { \lambda } = \sum _ { \mu } K _ { \lambda \mu } m _ { \mu }. \end{equation*}

Now consider the complete homogeneous symmetric functions $h_\lambda = h _ { \lambda _ { 1 } } \ldots h _ { \lambda _ { l } }$ and the elementary symmetric functions $\lambda = e _ { \lambda _ { 1 } } \cdots e _ { \lambda _ { l } }$, where $h _ { \lambda _ { i } }$ (respectively, $e _ { \lambda _ { i } }$) is the sum of all (respectively, all square-free) monomials of degree $\lambda _ { i }$. Also, let $\lambda ^ { \prime }$ denote the partition conjugate to $\lambda$, whose parts are the column lengths of $\lambda$'s shape. In the preceding example, $\lambda ^ { \prime } = ( 3,2,1,1 )$. For the two bases under consideration, the function $s_{ \lambda }$ can be described as a determinant (the Jacobi–Trudi identity [a2], [a12] and its dual):

\begin{equation*} s _ { \lambda } = \operatorname { det } ( h _ { \lambda _ { i } - i + j } ), \end{equation*}

\begin{equation*} s _ { \lambda ^ { \prime } } = \operatorname { det } ( e _ { \lambda _ { i } - i + j } ). \end{equation*}

Note that this identity immediately implies

\begin{equation*} s _{( l )} = h _ { l } \text { and } s _ { ( 1 ^ { l }) } = e_{ l}, \end{equation*}

where $( 1 ^ { l } )$ is the partition with $l$ parts all equal to $1$. These specializations also follow directly from the combinatorial definition of $s_{ \lambda }$.

Representations.

The description of $s_{ \lambda }$ in terms of the power sum symmetric functions brings in the representation theory of the symmetric group $\mathcal{S} _ { n }$. The irreducible representations of $\mathcal{S} _ { n }$ are indexed by partitions $\lambda$ such that $| \lambda | = n$. Given a conjugacy class of $\mathcal{S} _ { n }$ corresponding to a partition $\mu$, let $k _ { \mu }$ denote its size and let $\chi _ { \mu } ^ { \lambda }$ be the value of the $\lambda$th irreducible character on the class. Now consider the power sum symmetric function $p _ { \lambda } = p _ { \lambda _ { 1 } } \cdots p _ { \lambda _ { l } }$, where $p _ { \lambda _ { i } } = x _ { 1 } ^ { \lambda _ { i } } + \ldots + x _ { l } ^ { \lambda _ { i } }$.

The following now holds: If $| \lambda | = n$, then

\begin{equation*} s _ { \lambda } = \frac { 1 } { n ! } \sum _ { | \mu | = n } k _ { \mu } \chi _ { \mu } ^ { \lambda } p _ { \mu }. \end{equation*}

In other words, $s_{ \lambda }$ is the cycle-indicator generating function (in the sense of Polyá–Redfield enumeration) for the irreducible character of $\mathcal{S} _ { n }$ corresponding to $\lambda$.

Now, consider the complex general linear group $\operatorname{GL}_l$. A representation $\rho : \operatorname{GL} _ { l } \rightarrow \operatorname{GL} _ { m }$ is polynomial if, for every $X \in \operatorname {GL}_{l}$, the entries of $\rho ( X )$ are polynomials in the entries of $X$. The polynomial representations of $\operatorname{GL}_l$ are indexed by the partitions $\lambda$ with $l$ non-negative parts. Let 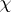be the character of a polynomial representation $\rho$ and let $X$ have eigenvalues $x _ { 1 } , \dots , x _ { l }$. Then 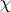is a polynomial function of the $x_{i}$ (because this is true for diagonalizable $X$ and these are dense in $\operatorname{GL}_l$) and is symmetric (because 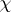is a class function). In fact, more is true: The irreducible polynomial characters of $\operatorname{GL}_l$ are precisely the $s_{ \lambda }$ for $\lambda$ with $l$ non-negative parts.

Properties.

The connection with representations of $\mathcal{S} _ { n }$ can be used to construct an isomorphism of algebras. Let $R ^ { n }$ denote the vector space of all class functions on $\mathcal{S} _ { n }$ and let $R = \sum _ { n > 0 } R ^ { n }$. The irreducible characters form a basis for $R$, and it can be endowed with a multiplication by induction of the tensor product. The characteristic or Frobenius mapping [a1] $\operatorname{ch} : R \rightarrow \Lambda$ is defined on $\chi \in R ^ { x }$ by

\begin{equation*} \operatorname { ch } ( \chi ) = \frac { 1 } { n ! } \sum _ { | \mu | = n } k _ { \mu } \chi _ { \mu } p _ { \mu }, \end{equation*}

where $\chi _ { \mu }$ is the value of 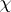on the class corresponding to $\mu$. The mapping $\operatorname{ch} : R \rightarrow \Lambda$ is an isomorphism of algebras. In fact, there are natural inner products on $R$ and $\Lambda$ that make $\operatorname{ch}$ an isometry.

A number of identities involving Schur functions have interesting bijective proofs using the combinatorial definition. Among the most famous are the following, in which it is assumed that $\mathbf{y} = \{ y _ { 1 } , \dots , y _ { l } \}$ is another set of variables.

The Cauchy identity and its dual are

\begin{equation*} \sum _ { \lambda } s _ { \lambda } ( \mathbf{x} ) s _ { \lambda } ( \mathbf{y} ) = \prod _ { i , j = 1 } ^ { l } \frac { 1 } { 1 - x _ { i } y _ { j } } \end{equation*}

and

\begin{equation*} \sum _ { \lambda } s _ { \lambda } ( \mathbf x ) s _ { \lambda ^ { \prime } } ( \mathbf y ) = \prod _ { i , j = 1 } ^ { l } ( 1 + x _ { i } y _ { j } ). \end{equation*}

D. Knuth [a4] has given algorithmic bijections between matrices and semi-standard Young tableaux that prove these identities. It is a generalization of a mapping of C. Schensted [a10] for standard Young tableaux, i.e., semi- standard Young tableaux where the entries are precisely $1 , \dots , | \lambda |$.

One can also describe the structure constants for the algebra $\Lambda$ in the basis $s_{ \lambda }$ combinatorially. If $\mu \subseteq \lambda$ as Ferrers shapes, then one has a skew shape $\lambda / \mu$ consisting of all dots or cells that are in $\lambda$ but not in $\mu$. Skew semi-standard Young tableaux are defined in the obvious way. The reverse row word for a semi-standard Young tableaux $T$, $\pi_T$, is obtained by reading the entries in each row from right to left, starting with the top row and working down. For the example tableau, $\pi_T = 3111324$. Also, a sequence of positive integers $\pi = w _ { 1 } \dots w _ { n }$ is a lattice permutation or ballot sequence if, in every prefix $w _ { 1 } \ldots w _ { k }$, the number of $i$'s is at least as big as the number of $( i + 1 )$'s for all $i \geq 1$. The Littlewood–Richardson rule [a7] states that if

\begin{equation*} \lambda ^ { s _ { \mu } } = \sum _ { \nu } c _ { \lambda \mu } ^ { \nu } s _ { \nu }, \end{equation*}

then $c _ { \lambda \mu } ^ { \nu }$ is equal to the number of semi-standard Young tableaux $T$ of shape $\nu / \lambda$ and content $\mu$ such that $\pi_T$ is a ballot sequence. Via the characteristic mapping, the Littlewood–Richardson coefficients $c _ { \lambda \mu } ^ { \nu }$ can also be viewed as giving the multiplicities of the character product $\chi ^ { \lambda } \chi ^ { \mu }$ when decomposed into irreducibles. Equivalently, one can consider the decomposition of the inner tensor product of two irreducible polynomial representations of $\operatorname{GL}_l$.

There are many generalizations of Schur functions, one of the most notable being the Hall–Littlewood functions. See [a8] for more information.

References

[a1]	F.G. Frobenius, "Über die Charactere der symmetrischen Gruppe" Sitz. K. Preuss. Akad. Wiss (1900) pp. 516–534 (Also: Gesammelte Abh. 3 Springer, 1968, 148-166)
[a2]	C. Jacobi, "De functionibus alternantibus earumque divisione per productum e differentiis elementorum conflatum" J. Reine Angew. Math. , 22 (1841) pp. 360–371 (Also: Math. Werke 3, Chelsea, 1969, 439-452)
[a3]	G.D. James, A. Kerber, "The representation theory of the symmetric group" , Encycl. Math. Appl. , 16 , Addison-Wesley (1981)
[a4]	D.E. Knuth, "Permutations, matrices and generalized Young tableaux" Pacific J. Math. , 34 (1970) pp. 709–727
[a5]	C. Kostka, "Über den Zusammenhang zwischen einigen Formen von symmetrischen Funktionen" Crelle's J. , 93 (1882) pp. 89–123
[a6]	D.E. Littlewood, "The theory of group characters" , Oxford Univ. Press (1950)
[a7]	D.E. Littlewood, A.R. Richardson, "Group characters and algebra" Philos. Trans. R. Soc. London Ser. A , 233 (1934) pp. 99–142
[a8]	I.G. Macdonald, "Symmetric functions and Hall polynomials" , Oxford Univ. Press (1995) (Edition: Second)
[a9]	B.E. Sagan, "The symmetric group: representations, combinatorial algorithms, and symmetric functions" , Wadsworth&Brooks/Cole (1991) (Second ed.: Springer, to appear)
[a10]	C. Schensted, "Longest increasing and decreasing subsequences" Canad. J. Math. , 13 (1961) pp. 179–191
[a11]	I. Schur, "Über eine Klasse von Matrizen die sich einer gegeben Matrix zuordnen lassen" Inaugural Diss. Berlin (1901)
[a12]	N. Trudi, "Intorno un determinante piu generale di quello che suol dirsi determinante delle radici di una equazione, ed alle funzioni simmetriche complete di queste radici" Rend. Accad. Sci. Fis. Mat. Napoli , 3 (1864) pp. 121–134 (Also: Giornale di Mat. 2 (1864), 152–158; 180–186)