Neumann eigenvalue

Consider a bounded domain $\Omega \subset \mathbf{R} ^ { n }$ with a piecewise smooth boundary $\partial \Omega$. A number $\mu$ is a Neumann eigenvalue of $\Omega$ if there exists a function $u \in C ^ { 2 } ( \Omega ) \cap C ^ { 0 } ( \overline { \Omega } )$ (a Neumann eigenfunction) satisfying the following Neumann boundary value problem (cf. also Neumann boundary conditions):

$$\begin{equation} \tag{a1} - \Delta u = \mu u \text { in } \Omega, \end{equation}$$

$$\begin{equation} \tag{a2} \frac { \partial u } { \partial n } = 0 \text { in } \partial \Omega, \end{equation}$$

where $\Delta$ is the Laplace operator (i.e., $\Delta = \sum _ { i = 1 } ^ { n } \partial ^ { 2 } / \partial x _ { i } ^ { 2 }$). For more general definitions, see [a8]. Neumann eigenvalues (with $n = 2$) appear naturally when considering the vibrations of a free membrane (cf. also Natural frequencies). In fact, for $n = 2$ the non-zero Neumann eigenvalues are proportional to the square of the eigenfrequencies of the membrane with free boundary. Provided $\Omega$ is bounded and the boundary $\partial \Omega$ is sufficiently regular, the Neumann Laplacian has a discrete spectrum of infinitely many non-negative eigenvalues with no finite accumulation point:

$$\begin{equation} \tag{a3} 0 = \mu _ { 1 } ( \Omega ) \leq \mu _ { 2 } ( \Omega ) \leq \dots \end{equation}$$

($\mu _ { k } \rightarrow \infty$ as $k \rightarrow \infty$). The Neumann eigenvalues are characterized by the max-min principle [a3]:

$$\begin{equation} \tag{a4} \mu _ { k } = \operatorname { sup } \operatorname { inf } \frac { \int _ { \Omega } ( \nabla u ) ^ { 2 } d x } { \int _ { \Omega } u ^ { 2 } d x }, \end{equation}$$

where the 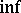is taken over all $u \in H ^ { 1 } ( \Omega )$ orthogonal to $\varphi _ { 1 } , \dots , \varphi _ { k - 1 } \in H ^ { 1 } ( \Omega )$, and the $\operatorname {sup}$ is taken over all the choices of $\{ \varphi _ { i } \} _ { i = 1 } ^ { k - 1 }$. For simply-connected domains the first eigenfunction $u_1$, corresponding to the eigenvalue $\mu _ { 1 } = 0$ is constant throughout the domain. All the other eigenvalues are positive. While Dirichlet eigenvalues satisfy stringent constraints (e.g., $\lambda _ { 2 } / \lambda _ { 1 }$ cannot exceed $2.539\dots$ for any bounded domain in $\mathbf{R} ^ { 2 }$, [a1]; see also Dirichlet eigenvalue), no such constraints exist for Neumann eigenvalues, other than the fact that they are non-negative. In fact, given any finite sequence $\mu _ { 1 } = 0 < \ldots < \mu _ { N }$, there is an open, bounded, smooth, simply-connected domain of $\mathbf{R} ^ { 2 }$ having this sequence as the first $N$ Neumann eigenvalues of the Laplacian on that domain [a2]. Though it is obvious from the variational characterization of both Dirichlet and Neumann eigenvalues (see (a4)) that $\mu _ { k } \leq \lambda _ { k }$, L. Friedlander [a4] proved the stronger result

$$\begin{equation} \tag{a5} \mu _ { k + 1 } \leq \lambda _ { k } ,\, k = 1, 2,\dots . \end{equation}$$

How far the first non-trivial Neumann eigenvalue is from zero for a convex domain in $\mathbf{R} ^ { 2 }$ is given through the optimal inequality [a7]

$$\begin{equation} \tag{a6} \mu _ { 1 } \geq \frac { \pi ^ { 2 } } { d ^ { 2 } }, \end{equation}$$

where $d$ is the diameter of the domain. There are many more isoperimetric inequalities for Neumann eigenvalues (see Rayleigh–Faber–Krahn inequality).

For large values of $k$, H. Weyl proved [a9]

$$\begin{equation} \tag{a7} \mu _ { k + 1 } \approx \frac { 4 \pi ^ { 2 } k ^ { 2 / n } } { ( C _ { n } | \Omega | ) ^ { 2 / n } }, \end{equation}$$

where $| \Omega |$ and $C _ { n } = \pi ^ { n / 2 } / \Gamma ( n / 2 + 1 )$ are, respectively, the volumes of $\Omega$ and of the unit ball in ${\bf R} ^ { n }$.

For any plane-covering domain (i.e., a domain that can be used to tile the plane without gaps, nor overlaps, allowing rotations, translations and reflections of itself), G. Pólya [a6] proved that

$$\begin{equation} \tag{a8} \mu _ { k + 1 } \leq \frac { 4 \pi k } { A } , k = 0,1 , \ldots , \end{equation}$$

and conjectured the same bound for any bounded domain in $\mathbf{R} ^ { 2 }$. This is equivalent to saying that the Weyl asymptotics of $\mu _ { k }$ is an upper bound for $\mu _ { k }$. The analogous conjecture in dimension $n$ is

$$\begin{equation} \tag{a9} \mu _ { k + 1 } \leq \frac { 4 \pi ^ { 2 } k ^ { 2 / n } } { ( C _ { n } | \Omega | ) ^ { 2 / n } } ,\, k = 0,1\dots. \end{equation}$$

The most significant result towards the proof of Pólya's conjecture for Neumann eigenvalues is the result by P. Kröger [a5]:

$$\begin{equation*} \sum _ { i = 1 } ^ { k } \mu _ { i } \leq \frac { n } { n + 2 } \frac { 4 \pi ^ { 2 } k ^ { 2 / n } } { ( C _ { n } | \Omega | ) ^ { 2 / n } } , k = 1,2, \dots . \end{equation*}$$

A proof of Pólya's conjecture for both Dirichlet and Neumann eigenvalues would imply Friedlander's result (a5).

References

[a1]	M.S. Ashbaugh, R.D. Benguria, "A sharp bound for the ratio of the first two eigenvalues of Dirichlet Laplacians and extensions" Ann. of Math. , 135 (1992) pp. 601–628
[a2]	Y. Colin de Vérdiere, "Construction de laplaciens dont une partie finie du spectre est donnée" Ann. Sci. École Norm. Sup. , 20 : 4 (1987) pp. 599–615
[a3]	R. Courant, D. Hilbert, "Methoden der mathematischen Physik" , I , Springer (1931) (English transl.: Methods of Mathematical Physics, vol. I., Interscience, 1953)
[a4]	L. Friedlander, "Some inequalities between Dirichlet and Neumann eigenvalues" Arch. Rational Mech. Anal. , 116 (1991) pp. 153–160
[a5]	P. Kröger, "Upper bounds for the Neumann eigenvalues on a bounded domain in Euclidean Space" J. Funct. Anal. , 106 (1992) pp. 353–357
[a6]	G. Polya, "On the eigenvalues of vibrating membranes" Proc. London Math. Soc. , 11 : 3 (1961) pp. 419–433
[a7]	L.E. Payne, H.F. Weinberger, "An optimal Poincaré inequality for convex domains" Arch. Rational Mech. Anal. , 5 (1960) pp. 286–292
[a8]	M. Reed, B. Simon, "Methods of modern mathematical physics IV: Analysis of operators" , Acad. Press (1978)
[a9]	H. Weyl, "Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen" Math. Ann. , 71 (1911) pp. 441–479