Radical in a class of semi-groups

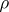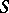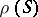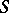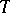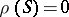A function associating to each semi-group a congruence (cf. Congruence (in algebra)) and having the following properties: 1) if is isomorphic to and (0 denotes the equality relation), then ; 2) if 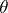is a congruence on 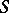and 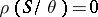, then 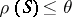; and 3) . If 1) and 3) are satisfied, then 2) is equivalent to

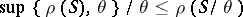for every congruence 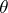on 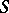. A semi-group 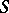is called 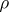-semi-simple if 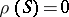. The class of -semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of 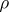-semi-simple semi-groups for some radical 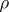. If 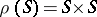, then 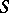is called 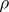-radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an ideal in each semi-group.

If 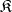is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group 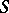the intersection of all congruences 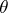such that 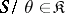turns out to be a radical, called 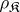. The class 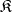coincides with the class of 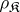-semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case is the largest quotient semi-group of 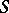that lies in 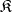(see Replica).

Example. Let 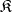be the class of semi-groups admitting a faithful irreducible representation (cf. Representation of a semi-group). Then

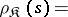where

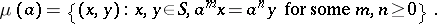Radicals defined on a given class of semi-groups that is closed relative to homomorphic images have been studied.

Related to each radical is the class of left polygons (cf. Polygon (over a monoid)). Namely, if is a left 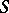-polygon, then a congruence 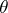on 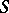is called -annihilating if implies 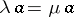for all 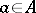. The least upper bound of all -annihilating congruences turns out to be an 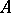-annihilating congruence, and is denoted by . The class 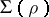, by definition, consists of all left 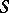-polygons 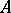such that , where 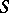runs through the class of all semi-groups. If 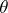is a congruence on 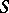, then a left 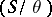-polygon lies in if and only if it lies in 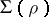when considered as a left 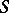-polygon. Conversely, if one is given a class 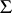of left polygons with these properties and if 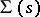is the class of all left 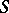-polygons in 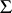, then the function

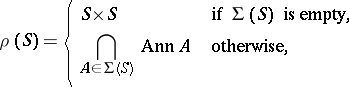is a radical.

References

[1]	A.H. Clifford, G.B. Preston, "The algebraic theory of semi-groups" , 2 , Amer. Math. Soc. (1967)
[2]	L.A. Skornyakov, "Radicals of -rings" , Selected problems in algebra and logic , Novosibirsk (1973) pp. 283–299 (In Russian)
[3]	A.H. Clifford, "Radicals in semigroups" Semigroup Forum , 1 : 2 (1970) pp. 103–127
[4]	E.N. Roiz, B.M. Schein, "Radicals of semigroups" Semigroup Forum , 16 : 3 (1978) pp. 299–344