Pseudo-Euclidean space
A real affine space in which to any vectors  and
and 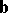 there corresponds a definite number, called the scalar product
there corresponds a definite number, called the scalar product 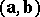 (cf. also Inner product), satisfying
(cf. also Inner product), satisfying
1) the scalar product is commutative:
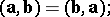 |
2) the scalar product is distributive with respect to vector addition:
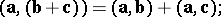 |
3) a scalar factor can be taken out of the scalar product:
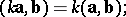 |
4) there exist  vectors
vectors 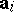 such that
such that
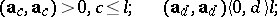 |
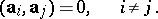 |
The number  is called the dimension of the pseudo-Euclidean space,
is called the dimension of the pseudo-Euclidean space, 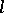 is called the index, the pair of numbers
is called the index, the pair of numbers 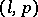 ,
, 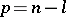 , is called the signature. A pseudo-Euclidean space is denoted by
, is called the signature. A pseudo-Euclidean space is denoted by 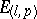 (or
(or 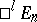 ). The space
). The space 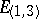 is called the Minkowski space. In any system of
is called the Minkowski space. In any system of  vectors
vectors 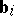 in
in 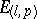 for which
for which 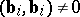 and
and 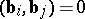 when
when 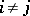 , the number of vectors
, the number of vectors 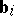 for which
for which 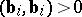 is equal to
is equal to 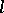 and the number of vectors
and the number of vectors 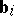 for which
for which 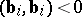 is equal to
is equal to 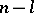 (the law of inertia for a quadratic form).
(the law of inertia for a quadratic form).
The modulus 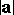 of a vector
of a vector  in a pseudo-Euclidean space can be defined as the non-negative root
in a pseudo-Euclidean space can be defined as the non-negative root 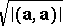 . The vectors that have scalar squares equal to 1 or
. The vectors that have scalar squares equal to 1 or 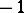 are called unit and pseudo-unit vectors, respectively. The vectors
are called unit and pseudo-unit vectors, respectively. The vectors  for which
for which 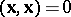 have zero modulus and are called isotropic vectors. The directions of the isotropic vectors are the isotropic directions.
have zero modulus and are called isotropic vectors. The directions of the isotropic vectors are the isotropic directions.
In a pseudo-Euclidean space there are three types of straight lines: Euclidean, having direction vector with positive scalar square 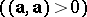 , pseudo-Euclidean
, pseudo-Euclidean 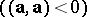 and isotropic
and isotropic 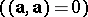 . The union of all the isotropic straight lines passing through a certain point is called the isotropic cone.
. The union of all the isotropic straight lines passing through a certain point is called the isotropic cone.
In a pseudo-Euclidean space there are several types of planes: Euclidean planes 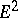 , pseudo-Euclidean planes
, pseudo-Euclidean planes 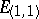 and planes containing isotropic vectors, the so-called semi-Euclidean planes with signatures
and planes containing isotropic vectors, the so-called semi-Euclidean planes with signatures 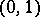 and
and 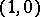 and deficiency 1 (see Semi-Euclidean space) and isotropic planes, all vectors of which are isotropic.
and deficiency 1 (see Semi-Euclidean space) and isotropic planes, all vectors of which are isotropic.
The distance between two points 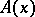 and
and 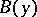 is taken to be the modulus of the vector
is taken to be the modulus of the vector 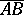 and is computed from:
and is computed from:
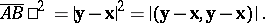 |
A pseudo-Euclidean space is not a metric space, since the triangle inequality is not satisfied. If the vectors  and
and 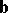 belong to a Euclidean plane (or to a pseudo-Euclidean plane of index 0), then they satisfy the triangle inequality, but if they belong to a pseudo-Euclidean plane of index 1, then they satisfy the so-called inverse triangle inequality:
belong to a Euclidean plane (or to a pseudo-Euclidean plane of index 0), then they satisfy the triangle inequality, but if they belong to a pseudo-Euclidean plane of index 1, then they satisfy the so-called inverse triangle inequality:
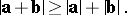 |
In a pseudo-Euclidean space there are three types of spheres: spheres with positive radius squared, 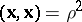 , spheres with negative radius squared,
, spheres with negative radius squared, 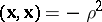 , and spheres of zero radius,
, and spheres of zero radius, 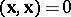 , which are just the isotropic cones.
, which are just the isotropic cones.
The motions of a pseudo-Euclidean space are affine transformations (cf. Affine transformation) and can be written in the form
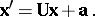 |
The operator 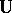 satisfies the condition
satisfies the condition  , that is, it preserves distances between points. The motions of a pseudo-Euclidean space form a multiplicative group; it depends on
, that is, it preserves distances between points. The motions of a pseudo-Euclidean space form a multiplicative group; it depends on 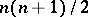 independent parameters. The motions of a pseudo-Euclidean space are called motions of the first or second kind if they are affine transformations of the corresponding kind.
independent parameters. The motions of a pseudo-Euclidean space are called motions of the first or second kind if they are affine transformations of the corresponding kind.
Geometric transformations are called anti-motions when each vector  goes to a vector
goes to a vector 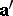 for which
for which 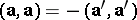 .
.
The basic operations of vector and tensor algebra can be introduced into a pseudo-Euclidean space. The basic differential-geometric concepts are constructed in accordance with the rules of the geometry of pseudo-Riemannian space. The metric tensor of a pseudo-Euclidean space has the form (in a Galilean coordinate system)
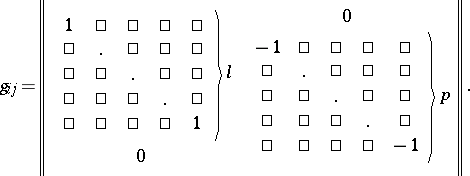 |
A pseudo-Euclidean space is flat, that is, its Riemann tensor is zero. If the Riemann tensor of a pseudo-Riemannian space is identically zero, then it is a locally pseudo-Euclidean space.
Subsets of a pseudo-Euclidean space can carry various metrics: A positive- or negative-definite Riemannian metric, a pseudo-Riemannian metric or a degenerate metric (see Indefinite metric). For example, the spheres of a pseudo-Euclidean space carry a (generally speaking, indefinite) metric of constant curvature. In 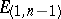 a sphere with positive radius squared is an
a sphere with positive radius squared is an 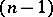 -dimensional space isometric to the hyperbolic space.
-dimensional space isometric to the hyperbolic space.
The pseudo-Euclidean space 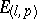 (
(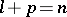 ) and the Euclidean space
) and the Euclidean space 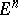 can be considered as subspaces of a complex space with form
can be considered as subspaces of a complex space with form 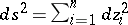 . If
. If 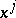 are coordinates in the pseudo-Euclidean space,
are coordinates in the pseudo-Euclidean space, 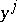 are those of the real Euclidean space and
are those of the real Euclidean space and 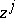 those of the complex Euclidean space, then the equations of the subspaces have the form
those of the complex Euclidean space, then the equations of the subspaces have the form
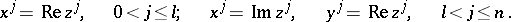 |
The metric of the pseudo-Euclidean space can be formally obtained from the metric of the Euclidean space by the substitution 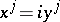 ,
, 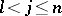 .
.
References
| [1] | N.V. Efimov, E.R. Rozendorn, "Linear algebra and multi-dimensional geometry" , Moscow (1970) (In Russian) |
| [2] | B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian) |
| [3] | L.D. Landau, E.M. Lifshitz, "The classical theory of fields" , Addison-Wesley (1962) (Translated from Russian) |
Comments
The concept of a pseudo-Euclidean space was generalized by E. Witt in 1937, see [a1]–[a2].
References
| [a1] | E. Witt, "Theorie der quadratischen Formen in beliebigen Körpern" J. Reine Angew. Math. , 176 (1937) pp. 31–44 |
| [a2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [a3] | S.W. Hawking, G.F.R. Ellis, "The large scale structure of space-time" , Cambridge Univ. Press (1973) |
| [a4] | C.W. Misner, K.S. Thorne, J.A. Wheeler, "Gravitation" , Freeman (1973) |
| [a5] | B. O'Neill, "Semi-Riemannian geometry (with applications to relativity)" , Acad. Press (1983) |
Pseudo-Euclidean space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-Euclidean_space&oldid=49380