Non-Abelian cohomology

Cohomology with coefficients in a non-Abelian group, a sheaf of non-Abelian groups, etc. The best known examples are the cohomology of groups, topological spaces and the more general example of the cohomology of sites (i.e. topological categories; cf. Topologized category) in dimensions 0, 1. A unified approach to non-Abelian cohomology can be based on the following concept. Let $C ^{0}$, $C ^{1}$ be groups, let $C ^{2}$ be a set with a distinguished point $e$, let $\mathop{\rm Aff}\nolimits \ C ^{1}$ be the holomorph of $C ^{1}$( i.e. the semi-direct product of $C ^{1}$ and $\mathop{\rm Aut}\nolimits ( C ^{1} )$; cf. also Holomorph of a group), and let $\mathop{\rm Aut}\nolimits \ C ^{2}$ be the group of permutations of $C ^{2}$ that leave $e$ fixed. Then a non-Abelian cochain complex is a collection $$C ^{*} = (C ^{0} ,\ C ^{1} ,\ C ^{2} ,\ \rho ,\ \sigma ,\ \delta ),$$ where $\rho : \ C ^{0} \rightarrow \mathop{\rm Aff}\nolimits \ C ^{1}$, $\sigma : \ C ^{0} \rightarrow \mathop{\rm Aut}\nolimits \ C ^{2}$ are homomorphisms and $\delta : \ C ^{1} \rightarrow C ^{2}$ is a mapping such that $$\delta (e) = e \textrm{ and } \delta ( \rho (a) b) = \sigma (a) \delta (b), a \in C ^{0} , b \in C ^{1} .$$ Define the $0$- dimensional cohomology group by $$H ^{0} (C ^{*} ) = \rho ^{-1} ( \mathop{\rm Aut}\nolimits \ C ^{1} ),$$ and the $1$- dimensional cohomology set (with distinguished point) by $$H ^{1} (C ^{*} ) = Z ^{1} / \rho ,$$ where $Z ^{1} = \delta ^{-1} (e) \subseteq C ^{1}$ and the factorization is modulo the action $\rho$ of the group $C ^{0}$.

Examples.

1) Let $X$ be a topological space with a sheaf of groups ${\mathcal F}$, and let $\mathfrak U$ be a covering of $X$; one then has the Čech complex $$C ^{*} ( \mathfrak U ,\ {\mathcal F} ) = (C ^{0} ( \mathfrak U ,\ {\mathcal F} ), C ^{1} ( \mathfrak U ,\ {\mathcal F} ), C ^{2} ( \mathfrak U ,\ {\mathcal F} )),$$ where $C ^{i} ( \mathfrak U ,\ {\mathcal F} )$ are defined as in the Abelian case (see Cohomology), $$( \sigma (a) (c)) _{ijk} = a _{i} c _{ijk} a _{i} ^{-1} ,$$ $$( \delta b) _{ijk} = b _{ij} b _{jk} b _{ik} ^{-1} ,$$ $$a \in C ^{0} , b \in C ^{1} , c \in C ^{2} .$$ Taking limits with respect to coverings, one obtains from the cohomology sets $H ^{i} (C ^{*} ( \mathfrak U ,\ {\mathcal F} ))$, $i = 0,\ 1$, the cohomology $H ^{i} (X,\ {\mathcal F} )$, $i = 0,\ 1$, of the space $X$ with coefficients in ${\mathcal F}$. Under these conditions, $H ^{0} (X,\ {\mathcal F} ) = {\mathcal F} (X)$. If ${\mathcal F}$ is the sheaf of germs of continuous mappings with values in a topological group $G$, then $H ^{1} (X,\ {\mathcal F} )$ can be interpreted as the set of isomorphism classes of topological principal bundles over $X$ with structure group $G$. Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal $G$- object.

2) Let $G$ be a group and let $A$ be a (not necessarily Abelian) $G$- group, i.e. an operator group with group of operators $G$. Denote the action of an operator $g \in G$ on an element $a \in A$ by $a ^{g}$. Define a complex $C ^{*} (G,\ A)$ by the formulas $$C ^{k} = \mathop{\rm Map}\nolimits (G ^{k} ,\ A), k = 0,\ 1,\ 2,$$ $$( \rho (a) (b)) (g) = ab (g) (a ^{g} ) ^{-1} ,$$ $$( \sigma (a) (c)) (g,\ h) = a ^{g} c (g,\ h) (a ^{g} ) ^{-1} ,$$ $$\delta (b) (g,\ h) = b (g) ^{-1} b (gh) (b (h) ^{g} ) ^{-1} ,$$ $$a \in C ^{0} , b \in C ^{1} , c \in C ^{2} , g \in G.$$ The group $H ^{0} (G,\ A) = H ^{0} (C ^{*} (G,\ A))$ is the subgroup $A ^{G}$ of $G$- fixed points in $A$, while $H ^{1} (G,\ A) = H ^{1} ( C ^{*} ( G ,\ A ) )$ is the set of equivalence classes of crossed homomorphisms $G \rightarrow A$, interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over $A$. For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.

3) Let $X$ be a smooth manifold, $G$ a Lie group and $\mathfrak g$ the Lie algebra of $G$. The non-Abelian de Rham complex $R _{G} ^{*} (X)$ is defined as follows: $R _{G} ^{0} (X)$ is the group of all smooth functions $X \rightarrow G$; $R _{G} ^{k} (X)$, $k = 1,\ 2$, is the space of exterior $k$- forms on $X$ with values in $\mathfrak g$; $$\rho (f \ ) ( \alpha ) = df \cdot f ^ {\ -1} + ( \mathop{\rm Ad}\nolimits \ f \ ) \alpha ;$$ $$\sigma (f \ ) ( \beta ) = ( \mathop{\rm Ad}\nolimits \ f \ ) \beta ,$$ $$\delta \alpha = d \alpha - { \frac{1}{2} } [ \alpha ,\ \alpha ],$$ $$f \in R _{G} ^{0} , a \in R _{G} ^{1} , \beta \in R _{G} ^{2} .$$ The set $H ^{1} (R _{G} (X))$ is the set of classes of totally-integrable equations of the form $df \cdot f ^ {\ -1} = \alpha$, $\alpha \in R _{G} ^{1}$, modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set $H ^{1} ( \pi _{1} (M),\ G)$ of conjugacy classes of homomorphisms $\pi _{1} (M) \rightarrow G$. In the case of a complex manifold $M$ and a complex Lie group $G$, one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.

For each subcomplex of a non-Abelian cochain complex there is an associated exact cohomology sequence. For example, for the complex $C ^{*} (G,\ A)$ of Example 2 and its subcomplex $C ^{*} (G,\ B)$, where $B$ is a $G$- invariant subgroup of $A$, this sequence is $$e \rightarrow H ^{0} (G,\ B) \rightarrow H ^{0} (G,\ A) \rightarrow (A/B) ^{G } \rightarrow$$ $$\rightarrow H ^{1} (G,\ B) \rightarrow H ^{1} (G,\ A).$$ If $B$ is a normal subgroup of $A$, the sequence can be continued up to the term $H ^{1} (G,\ A/B)$, and if $B$ is in the centre it can be continued to $H ^{2} (G,\ B)$. This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.

Apart from the 0- and $1$- dimensional non-Abelian cohomology groups just described, there are also $2$- dimensional examples. A classical example is the $2$- dimensional cohomology of a group $G$ with coefficients in a group $A$; the definition is as follows. Let ${\mathcal Z} ^{2} (G,\ A)$ denote the set of all pairs $(m,\ \phi )$, where $m: \ G \times G \rightarrow A$, $\phi : \ G \rightarrow \mathop{\rm Aut}\nolimits \ A$ are mappings such that $$\phi (g _{1} ) \phi (g _{2} ) \phi (g _{1} g _{2} ) ^{-1} = \mathop{\rm Int}\nolimits \ m (g _{1} ,\ g _{2} ),$$ $$m (g _{1} ,\ g _{2} ) m (g _{1} g _{2} ,\ g _{3} ) = \phi (g _{1} ) (m (g _{2} ,\ g _{3} )) m (g _{1} ,\ g _{2} \ g _{3} );$$ here $\mathop{\rm Int}\nolimits \ a$ is the inner automorphism generated by the element $a \in A$. Define an equivalence relation in ${\mathcal Z} ^{2} (G,\ A)$ by putting $(m,\ \phi ) \sim (m ^ \prime ,\ \phi ^ \prime )$ if there is a mapping $h: \ G \rightarrow A$ such that $$\phi ^ \prime (g) = ( \mathop{\rm Int}\nolimits \ h (g)) \phi (g)$$ and $$m ^ \prime (g _{1} ,\ g _{2} ) = h (g _{1} ) ( \phi (g _{1} ) (h (g _{2} ))) m (g _{1} ,\ g _{2} ) h (g _{1} ,\ g _{2} ) ^{-1} .$$ The equivalence classes thus obtained are the elements of the cohomology set ${\mathcal H} ^{2} (G,\ A)$. They are in one-to-one correspondence with the equivalence classes of extensions of $A$ by $G$( see Extension of a group).

The correspondence $(m,\ \phi ) \rightarrow \phi$ gives a mapping $\theta$ of the set ${\mathcal H} ^{2} (G,\ A)$ into the set of all homomorphisms $$G \rightarrow \mathop{\rm Out}\nolimits \ A = \mathop{\rm Aut}\nolimits \ A/ \mathop{\rm Int}\nolimits \ A;$$ let $H _ \alpha ^{2} (G,\ A) = \theta ^{-1} ( \alpha )$ for $\alpha \in \mathop{\rm Out}\nolimits \ A$. If one fixes $\alpha \in \mathop{\rm Out}\nolimits \ A$, the centre $Z (A)$ of $A$ takes on the structure of a $G$- module and so the cohomology groups $H ^{k} (G,\ Z (A))$ are defined. It turns out that $H _ \alpha ^{2} (G,\ A)$ is non-empty if and only if a certain class in $H ^{3} (G,\ Z (A))$ is trivial. Moreover, under this condition the group $H ^{2} (G,\ Z (A))$ acts simplely transitively on the set $H _ \alpha ^{2} (G,\ A)$.

This definition of a two-dimensional cohomology can be generalized, carrying it over to sites (see [2], where the applications of this concept are also presented). A general algebraic scheme that yields a two-dimensional cohomology is outlined in [4]; just as in the special case described above, computation of two-dimensional cohomology reduces to the computation of one-dimensional non-Abelian and ordinary Abelian cohomology.

References

[1]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) MR0180551 Zbl 0128.26303
[2]	J. Giraud, "Cohomologie non abélienne" , Springer (1971) MR0344253 Zbl 0226.14011
[3]	A.L. Onishchik, "Some concepts and applications of the theory of non-Abelian cohomology" Trans. Moscow Math. Soc. , 17 (1979) pp. 49–98 Trudy Moskov. Mat. Obshch. , 17 (1967) pp. 45–88
[4]	A.K. Tolpygo, "Two-dimensional cohomologies and the spectral sequence in the nonabelian theory" Selecta Math. Sov. , 6 (1987) pp. 177–197 MR0548342 Zbl 0619.18006
[5]	P. Dedecker, "Three-dimensional nonabelian cohomology for groups" , Category theory, homology theory and their applications (Battelle Inst. Conf.) , 2 , Springer (1968) pp. 32–64
[6]	J. Frenkel, "Cohomology non abélienne et espaces fibrés" Bull. Soc. Math. France , 85 : 2 (1957) pp. 135–220
[7]	H. Goldschmidt, "The integrability problem for Lie equations" Bull. Amer. Math. Soc. , 84 : 4 (1978) pp. 531–546 MR0517116 Zbl 0439.58025
[8]	T.A. Springer, "Nonabelian 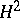in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182 MR209297 Zbl 0193.48902