User:Maximilian Janisch/latexlist/Algebraic Groups/Lie theorem

This page is a copy of the article Lie theorem in order to test automatic LaTeXification. This article is not my work.

Lie's theorem is one of the three classical theorems in the theory of Lie groups that describe the connection between a local Lie group (cf. Lie group, local) and its Lie algebra. Lie's theorems are the foundations of the theory developed in the 19th century by S. Lie and his school (see ).

Let $k$ be an $N$-dimensional real effective local Lie transformation group of a domain $\Omega \subset R ^ { x }$, let $E$ be the identity of $k$ and suppose that in local coordinates in a neighbourhood of the set $\{ e \} \times \Omega$ in $G \times \Omega$ the action of $k$ on $S$ is given by a system of analytic functions

\begin{equation} y _ { i } = f _ { i } ( g _ { 1 } , \ldots , g _ { i } ; x _ { 1 } , \ldots , x _ { n } ) , \quad i = 1 , \ldots , n \end{equation}

where $g = ( g 1 , \ldots , g _ { v } ) \in G$, $x = ( x _ { 1 } , \ldots , x _ { x } ) \in \Omega$ and $g ( x ) = y = ( y _ { 1 } , \ldots , y _ { x } ) \in \Omega$. This action defines $N$ analytic vector fields on $S$,

\begin{equation} X _ { i } = \sum _ { j = 1 } ^ { n } \xi _ { i j } ( x ) \frac { \partial } { \partial x _ { j } } , \quad i = 1 , \ldots , r \end{equation}

where $\xi _ { i j } ( x ) = \partial f _ { j } / \partial g ( e , x )$.

Lie's first theorem establishes that the functions $f$, $j = 1 , \ldots , n$, which define the action of $k$ are themselves defined by some auxiliary system of analytic functions $\psi _ { k i } ( g )$, $k , i = 1 , \dots , r$, on $k$ which satisfy the condition

\begin{equation} \psi _ { k i } ( e ) = \delta _ { k i } \end{equation}

where $\delta _ { k j }$ is the Kronecker symbol. More precisely, $( \psi _ { k i } ( g ) )$ is the matrix of the differential of the right translation of $k$ by the element $g ^ { - 1 }$ at the point 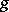, and the system of functions (1) is precisely the solution of the system of equations

\begin{equation} \frac { \partial f _ { j } } { \partial g _ { i } } ( g , x ) = \sum _ { k = 1 } ^ { r } \xi _ { k j } ( f ( g _ { s } x ) ) \psi _ { k i } ( g ) \end{equation}

\begin{equation} i = 1 , \ldots , r , \quad j = 1 , \ldots , n \end{equation}

that satisfies the initial conditions $f _ { j } ( e , x ) = x$, $j = 1 , \ldots , n$.

Lie's second theorem describes the properties of the functions $\xi _ { i j } ( x )$ and $\psi _ { k i } ( x )$. Namely, the $\xi _ { i j } ( x )$ satisfy the system of equations

\begin{equation} \sum _ { k = 1 } ^ { N } ( \xi _ { i k } \frac { \partial \xi _ { j l } } { \partial x _ { k } } - \xi _ { j k } \frac { \partial \xi _ { i l } } { \partial x _ { k } } ) = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } \xi _ { k l } \end{equation}

\begin{equation} 1 \leq i , j \leq r , \quad 1 \leq l \leq n \end{equation}

(this system is the condition that the system (4) is integrable), and the functions $\psi _ { k i } ( g )$ satisfy the system of equations

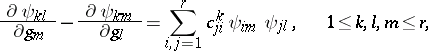where the $c _ { i j } ^ { k }$ are certain constants. The relations (5) imply that the commutator (Lie bracket) $[ X _ { i } , X _ { j } ]$ of two vector fields $X$ and $X$ is a linear combination of the fields $X _ { 1 } , \ldots , X _ { r }$ with constant coefficients:

\begin{equation} [ X _ { i } , X _ { j } ] = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } X _ { k } \end{equation}

that is, the linear hull $8$ of the fields $X _ { 1 } , \ldots , X _ { r }$ is an algebra with respect to the Lie bracket.

The converse of Lie's first and second theorems is the following: If the functions $f _ { 1 } , \ldots , f _ { x }$ give a solution of (4) in which the matrix $\| \xi _ { i j } \|$ has maximal rank and if (3) and (5) are satisfied, then (1) determines a local effective Lie transformation group. This local group is generated by the one-parameter transformation groups given by (2).

Lie's third theorem asserts that the constants $c _ { i j } ^ { k }$ satisfy the following relations:

\begin{equation} \left. \begin{array} { c } { c _ { i j } ^ { k } = - c _ { j i } ^ { k } } \\ { \sum _ { l = 1 } ^ { r } ( c _ { i l } ^ { m } c _ { j k } ^ { l } + c _ { k l } ^ { m } c _ { i j } ^ { l } + c _ { j l } ^ { m } c _ { k i } ^ { l } ) = 0 , \quad 1 \leq i , j , k , l , m \leq r } \end{array} \right. \end{equation}

that is, $8$ is a Lie algebra. The converse of the third theorem is important: If the $c _ { i j } ^ { k }$ are any constants satisfying (7), then there is a system of vector fields $X _ { 1 } , \ldots , X _ { r }$ satisfying (6), and these vector fields arise by means of the construction described above from some local Lie transformation group (in other words, every finite-dimensional Lie algebra is the Lie algebra of some local Lie transformation group). Lie's third theorem is sometimes (see , for example) taken to be the assertion about the existence, for every finite-dimensional Lie algebra $8$ over $R$ or $m$, of a global Lie group with Lie algebra $8$ (see Lie algebra of an analytic group).

Lie's theorem on solvable Lie algebras: Let $( 1 )$ be a linear representation of a finite-dimensional solvable Lie algebra (cf. Lie algebra, solvable) $1$ in a vector space $V$ over an algebraically closed field of characteristic 0; then there is a basis of $V$ in which all the operators $x$ of $\phi ( b )$ are written as upper triangular matrices. A similar assertion is true for a linear continuous representation of a connected topological solvable group in a finite-dimensional complex vector space (the group-theoretic analogue of Lie's theorem); the assumption that the group is connected is essential. A version of the group-theoretic analogue of Lie's theorem is known as the Lie–Kolchin theorem.

References

[1]	S. Lie, F. Engel, "Theorie der Transformationsgruppen" , 1–3 , Leipzig (1888–1893) MR1510035 Zbl 50.0002.01 Zbl 53.0026.07 Zbl 25.0626.01 Zbl 25.0623.01 Zbl 23.0376.01 Zbl 22.0372.01 Zbl 23.0364.01 Zbl 20.0368.01 Zbl 21.0356.02 Zbl 16.0326.01 Zbl 12.0292.01 Zbl 11.0258.02 Zbl 10.0260.01 Zbl 10.0258.01
[2]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002
[3]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104
[4]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803
[5]	C. Chevalley, "Théorie des groupes de Lie" , 3 , Hermann (1955) MR0068552 Zbl 0186.33104 Zbl 0054.01303 Zbl 0063.00843
[6]	N.G. Chebotarev, "The theory of Lie groups" , Moscow-Leningrad (1940) (In Russian)

Comments

For part 1) of the main article above see also Frobenius theorem on Pfaffian systems.

References

[a1]	A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201
[a2]	V.S. Varadarajan, "Lie groups, Lie algebras, and their representations" , Prentice-Hall (1974) MR0376938 Zbl 0371.22001
[a3]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. 121 MR0514561 Zbl 0451.53038