Injective module

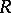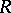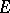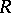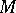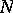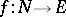An injective object in the category of (right) modules over an associative ring with identity , i.e. an -module such that for any -modules , , for any monomorphism , and for any homomorphism there is a homomorphism 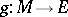that makes the following diagram commutative

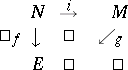Here and below all 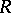-modules are supposed to be right 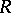-modules. The following conditions on an 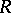-module 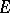are equivalent to injectivity: 1) for any exact sequence

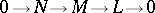the induced sequence

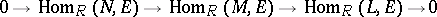is exact; 2) any exact sequence of 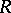-modules of the form

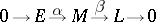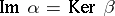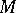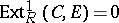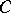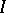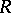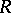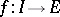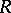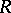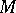splits, i.e. the submodule is a direct summand of ; 3) for all -modules ; and 4) for any right ideal of a homomorphism of -modules can be extended to a homomorphism of -modules (Baer's criterion). There are "enough" injective objects in the category of -modules: Each -module can be imbedded in an injective module. Moreover, each module 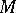has an injective evelope 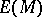, i.e. an injective module containing 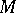in such a way that each non-zero submodule of 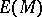has non-empty intersection with 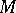. Any imbedding of a module 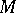into an injective module 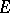can be extended to an imbedding of 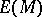into 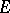. Every 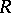-module 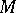has an injective resolution

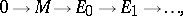i.e. an exact sequence of modules in which each module 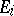, , 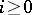is injective. The length of the shortest injective resolution is called the injective dimension of the module (cf. also Homological dimension).

A direct product of injective modules is an injective module. An injective module 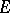is equal to 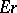for any 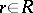that is not a left zero divisor in 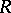, i.e. an injective module is divisible. In particular, an Abelian group is an injective module over the ring 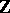if and only if it is divisible. Let 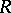be a commutative Noetherian ring. Then any injective module over it is a direct sum of injective hulls of modules of the form 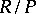, where 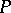is a prime ideal in .

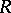Injective modules are extensively used in the description of various classes of rings (cf. Homological classification of rings). Thus, all modules over a ring are injective if and only if the ring is semi-simple. The following conditions are equivalent: is a right Noetherian ring; any direct sum of injective 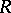-modules is injective; any injective 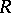-module is decomposable as a direct sum of indecomposable 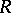-modules. A ring 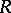is right Artinian if and only if every injective module is a direct sum of injective hulls of simple modules. A ring 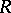is right hereditary if and only if all its quotient modules by injective 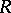-modules are injective, and also if and only if the sum of two injective submodules of an arbitrary 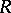-module is injective. If the ring 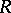is right hereditary and right Noetherian, then every -module contains a largest injective submodule. The projectivity (injectivity) of all injective (projective) 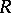-modules is equivalent to 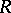being a quasi-Frobenius ring.

The injective hull of the module 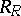plays an important role in the theory of rings of fractions. E.g., if the right singular ideal of a ring 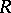vanishes, if 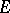is the injective hull of the module 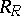, and if 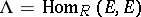is its endomorphism ring, then the 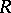-modules 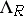and 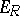are isomorphic, is a ring isomorphic to 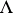and is also the maximal right ring of fractions of 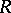, and 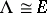is a self-injective right regular ring (in the sense of von Neumann).

In connection with various problems on extending module homomorphisms, some classes of modules 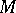close to injective modules have been considered: quasi-injective modules (if 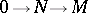and 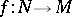, then can be extended to an endomorphism of 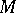); pseudo-injective modules (if 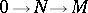and 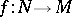is a monomorphism, then 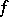can be extended to an endomorphism of 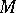); and small-injective modules (all endomorphisms of submodules can be extended to endomorphisms of 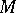). The quasi-injectivity of a module 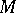is equivalent to the invariance of 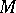in its injective hull under endomorphisms of the latter.

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[2]	S. MacLane, "Homology" , Springer (1963)
[3]	C. Faith, "Lectures on injective modules and quotient rings" , Springer (1967)
[4]	D.W. Sharpe, P. Vamos, "Injective modules" , Cambridge Univ. Press (1972)

Comments

A ring is called right hereditary if every right ideal is projective or, equivalently, if its right global dimension is 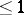. It is called semi right hereditary if every finitely-generated right ideal is projective. Commutative hereditary integral domains are Dedekind rings; a commutative semi-hereditary integral domain is called a Prüfer ring. A right hereditary ring need not be also left hereditary.

References

[a1]	C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973)
[a2]	J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) pp. Part I, Chapt. 2