Lie algebra, local
A Lie algebra whose elements are smooth functions on a smooth real manifold  (or, more generally, are smooth sections of a smooth vector bundle
(or, more generally, are smooth sections of a smooth vector bundle  over
over  ), and the commutation operation is continuous in the
), and the commutation operation is continuous in the  -topology and has a local character, that is,
-topology and has a local character, that is,
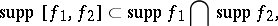 |
where  is the support of the function (section)
is the support of the function (section)  . A complete classification of local Lie algebras is known for bundles
. A complete classification of local Lie algebras is known for bundles  with one-dimensional fibre (in particular, for ordinary functions) (see [3]). Namely, the commutation operation in this case is a bidifferential operator of the first order, that is, it has the form
with one-dimensional fibre (in particular, for ordinary functions) (see [3]). Namely, the commutation operation in this case is a bidifferential operator of the first order, that is, it has the form
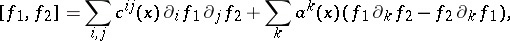 |
where  are the partial derivatives with respect to local coordinates on
are the partial derivatives with respect to local coordinates on  . Next, let
. Next, let  be the subspace of the tangent space
be the subspace of the tangent space 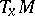 to
to  at a point
at a point 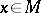 generated by the vectors
generated by the vectors
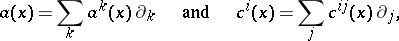 |
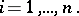 |
Then the distribution  is integrable, so
is integrable, so  decomposes into the union
decomposes into the union  of integral manifolds. The commutation operation commutes with restriction to
of integral manifolds. The commutation operation commutes with restriction to  , and the structures of local Lie algebras that arise in this way on
, and the structures of local Lie algebras that arise in this way on 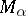 are transitive in the sense that
are transitive in the sense that  , for any point
, for any point  , coincides with the tangent space to the integral manifold
, coincides with the tangent space to the integral manifold  containing
containing  .
.
Every transitive local Lie algebra is defined locally by the dimension of the underlying manifold up to a change of variables in the base and fibre. For an even-dimensional manifold it is isomorphic to the algebra of Poisson brackets, and for odd-dimensional manifolds it is isomorphic to the algebra of Lagrange brackets (cf. Lagrange bracket, see also [1]).
An example of a local Lie algebra that illustrates the general theory is the structure of the Lie algebra in  in which
in which
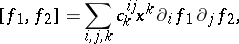 |
where 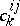 are the structure constants of an
are the structure constants of an  -dimensional Lie algebra
-dimensional Lie algebra  (see [2]). In this case the manifold
(see [2]). In this case the manifold 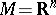 is naturally identified with the space
is naturally identified with the space  dual to
dual to 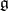 , and the partition into submanifolds
, and the partition into submanifolds 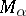 coincides with the partition of
coincides with the partition of 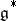 into orbits of the coadjoint representation.
into orbits of the coadjoint representation.
Local Lie algebras arise as the Lie algebras of certain infinite-dimensional Lie groups. In particular, they are Lie algebras of differential groups in the sense of J.F. Ritt [4]. From [5] there follows a description of all local Lie algebras connected with bundles on a line with two-dimensional fibre. All such local Lie algebras are extensions of the algebra of Lagrange brackets (which in this case coincides with the Lie algebra of vector fields) by means of a trivial local Lie algebra with one-dimensional fibre. A classification of "simple" local Lie algebras has been announced [6].
References
| [1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [2] | F.A. Berezin, "Some remarks about the associative envelope of a Lie algebra" Funct. Anal. Appl. , 1 : 2 (1967) pp. 91–102 Funktsional. Anal. i Prilozhen. , 1 : 2 (1967) pp. 1–14 |
| [3] | A.A. Kirillov, "Local Lie algebras" Russian Math. Surveys , 31 : 4 (1976) pp. 55–75 Uspekhi Mat. Nauk , 31 : 4 (1976) pp. 57–76 |
| [4] | J.F. Ritt, "Differential groups and formal Lie theory for an infinite number of variables" Ann. of Math. (2) , 52 (1950) pp. 708–726 |
| [5] | J.F. Ritt, "Differential groups of order two" Ann. of Math. (2) , 53 (1951) pp. 491–519 |
| [6] | B. Weisfeiler, "On Lie algebras of differential formal groups of Ritt" Bull. Amer. Math. Soc. , 84 : 1 (1978) pp. 127–130 |
Comments
For an account of the role of local Lie algebras (and related structures) in the deformation-theoretic approach to quantization cf. [a1].
References
| [a1] | A. Lichnerowicz, "Applications of the deformations of algebraic structures to geometry and mathematical physics" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 855–896 |
Lie algebra, local. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_local&oldid=39342