Equivalence problem for systems of second-order ordinary differential equations

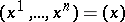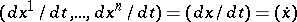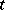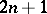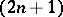Let , , and be coordinates in an open connected subset of the Euclidean -dimensional space 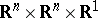. Suppose that there is given a second-order system

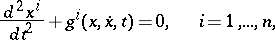(a1)

for which each 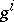is 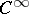in a neighbourhood of initial conditions .

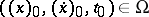Following D. Kosambi [a8], one wishes to solve the problem of finding the intrinsic geometric properties (i.e., the basic differential invariants) of (a1) under non-singular coordinate transformations of the type

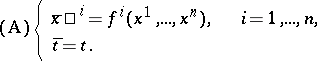A similar problem was solved by E. Cartan and S.S. Chern [a4], [a5], but in the real-analytic case with transformations 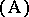replaced by

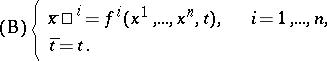Below, only 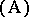is considered; see the references for .

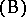Define the KCC-covariant differential of a contravariant vector field 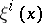on by

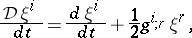(a2)

where the semi-colon indicates partial differentiation with respect to . Note that the Einstein summation convention on repeated upper and lower indices is used throughout. Using (a2), equation (a1) can be re-expressed as

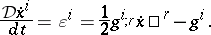(a3)

The quantity 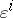is a contravariant vector field on and constitutes the first KCC-invariant of (a1). It represents an "external force" .

If the trajectories 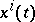of (a1) are varied into nearby ones according to

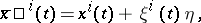(a4)

where 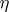denotes a constant with 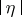small and the 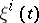are the components of some contravariant vector defined along 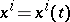, substitution of (a4) into (a1) and taking the limit as 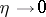results in the variational equations

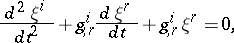(a5)

where the comma indicates partial differentiation with respect to 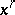. Using the KCC-covariant differential (a2), this can be re-expressed as

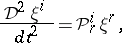(a6)

where

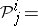(a7)

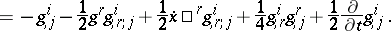The tensor 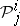is the second KCC-invariant of (a1). The third, fourth and fifth invariants are:

(a8)

The main result of KCC-theory is the following assertion: Two systems of the form (a1) on are equivalent relative to 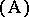if and only if the five KCC-invariant tensors 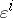, , 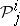, , 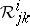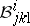and 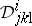are equivalent. In particular, there exist coordinates 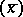for which the 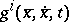all vanish if and only if all KCC-invariants are zero.

Remarks.

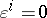if and only if 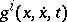are positively homogeneous of degree two in the variable 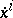. In this case, the structure of must accommodate possible non-differentiability in . This happens in Finsler geometry, but not in affine and Riemannian geometries, where (a1) are geodesics or autoparallels of a linear connection whose coefficients are 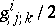. The latter are known as the coefficients of the Berwald connection in Finsler geometry, and of the Levi-Civita connection for Riemannian theory [a3], [a9], [a10]. Furthermore, in the Finsler case, 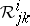, 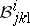are the Berwald torsion and curvature tensors. Also, 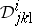is the Douglas tensor, whose vanishing is necessary and sufficient for all 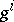to be quadratic in the variables . The latter is always zero in Riemannian and affine geometries, and also for Berwald spaces in Finsler theory [a6], [a3].

Finally, the KCC-invariants can be readily computed in each of the two following cases:

1)

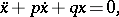whe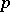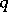re , are 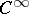functions of 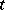only. In this case 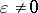and

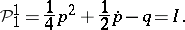The trajectories of this equation are Lyapunov stable if 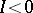, and unstable if ;

2)

where are the coefficients of the Levi-Civita connection of a two-dimensional Riemannian metric, are fixed constants and where the bracket on the right-hand side indicates no summation, [a3]. The KCC-invariants in the case where are close to Riemannian, but 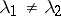has a significant effect on Lyapunov stability.

Further applications of KCC-theory can be found in [a2], [a1]. The equivalence problem can be found in a more general context in [a7], [a11].

References

[a1]	P.L. Antonelli, P. Auger, "Aggregation and emergence in population dynamics" Math. Compt. Mod. , 27 : 4 (1998) (Edited volume)
[a2]	P.L. Antonelli, R.H. Bradbury, "Volterra–Hamilton models in the ecology and evolution of colonial organisms" , World Sci. (1996)
[a3]	P.L. Antonelli, R.S. Ingarden, M. Matsumoto, "The theory of sprays and finsler spaces with applications in physics and biology" , Kluwer Acad. Publ. (1993) pp. 350
[a4]	E. Cartan, "Observations sur le mémoire précédent" Math. Z. , 37 (1933) pp. 619–622
[a5]	S. Chern, "Sur la géométrie d'un système d'équations differentielles du second ordre" Bull. Sci. Math. II , 63 (1939) pp. 206–212 (Also: Selected Papers, Vol. II, Springer 1989, 52–57)
[a6]	J. Douglas, "The general geometry of paths" Ann. of Math. , 29 (1928) pp. 143–169
[a7]	R.B. Gardner, "The method of equivalence and its application" , CBMS , 58 , SIAM (Soc. Industrial Applied Math.) (1989)
[a8]	D. Kosambi, "Parallelism and path-spaces" Math. Z. , 37 (1933) pp. 608–618
[a9]	E. Kreyszig, "Introduction to differential and Riemannian geometry" , Univ. Toronto Press (1968)
[a10]	D. Laugwitz, "Differential and Riemannian geometry" , Acad. Press (1965)
[a11]	P.J. Olver, "Equivalence, invariants, and symmetry" , Cambridge Univ. Press (1995)
[a12]	D. Kosambi, "Systems of differential equations of second order" Quart. J. Math. Oxford , 6 (1935) pp. 1–12