Matrix Viète theorem
matrix Vieta theorem
The standard (scalar) Viète formulas express the coefficients of an equation
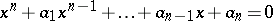 | (a1) |
in terms of the roots: up to sign, 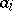 is the
is the 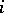 th elementary symmetric function of the roots
th elementary symmetric function of the roots  . See also Viète theorem.
. See also Viète theorem.
Consider now a matrix equation
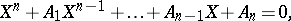 | (a2) |
where the solutions 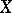 and coefficients
and coefficients 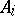 are square complex matrices. A set of
are square complex matrices. A set of  square matrices
square matrices 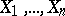 of size
of size 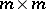 is called independent if the block Vandermonde determinant
is called independent if the block Vandermonde determinant
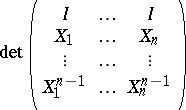 |
does not vanish. The matrix Viète theorem gives formulas for 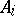 in terms of quasi-determinants, [a3], [a4], involving
in terms of quasi-determinants, [a3], [a4], involving  independent solutions of (a2), [a1], [a2]. In particular, if
independent solutions of (a2), [a1], [a2]. In particular, if 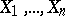 are
are  independent solutions of (a2), then
independent solutions of (a2), then
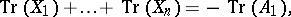 |
 |
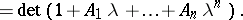 |
This theorem generalizes to the case of equations in an arbitrary associative ring (cf. also Associative rings and algebras), with an adequate notion of trace and determinant, see [a1], [a2].
References
| [a1] | A. Connes, A. Schwarz, "Matrix Vieta theorem revisited" Lett. Math. Phys. , 39 : 4 (1997) pp. 349–353 |
| [a2] | D. Fuchs, A. Schwarz, "Matrix Vieta theorem" Amer. Math. Soc. Transl. (2) , 169 (1995) pp. 15–22 |
| [a3] | I.M. Gel'fand, D. Krob, A. Lascoux, B. Leclerc, V.S. Redakh, J.Y. Thibon, "Noncomutative symmetric functions" Adv. Math. , 112 (1995) pp. 218–348 |
| [a4] | I.M. Gel'fand, V.S. Redakh, "A theory of noncommutative determinants and characteristic functions of graphs I" Publ. LACIM (Univ. Quebec) , 14 pp. 1–26 |
Matrix Viète theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_Vi%C3%A8te_theorem&oldid=35328