Adjoint linear transformation

of a linear transformation

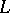The linear transformation on a Euclidean space (or unitary space) such that for all , the equality

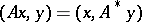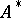between the scalar products holds. This is a special case of the concept of an adjoint linear mapping. The transformation is defined uniquely by . If is finite-dimensional, then every has an adjoint , the matrix 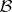of which in a basis is related to the matrix of 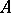in the same basis as follows:

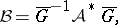where 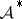is the matrix adjoint to 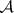and 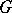is the Gram matrix of the basis .

In a Euclidean space, and 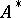have the same characteristic polynomial, determinant, trace, and eigen values. In a unitary space, their characteristic polynomials, determinants, traces, and eigen values are complex conjugates.

Comments

More generally, the phrase "adjoint transformation" or "adjoint linear mappingadjoint linear mapping" is also used to signify the dual linear mapping 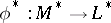of a linear mapping 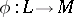. Here 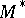is the space of (continuous) linear functionals on 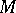and 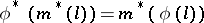. The imbeddings 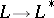, , 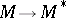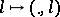connect the two notions. Cf. also Adjoint operator.

References

[a1]	M. Reed, B. Simon, "Methods of modern mathematical physics" , 1. Functional analysis , Acad. Press (1972) pp. Sect. 2