Kummer theorem
Let 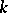 be the field of fractions of a Dedekind ring
be the field of fractions of a Dedekind ring 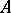 , let
, let 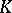 be an extension (cf. Extension of a field) of
be an extension (cf. Extension of a field) of 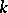 of degree
of degree  , let
, let 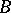 be the integral closure of
be the integral closure of 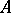 in
in 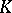 , and let
, and let 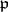 be a prime ideal in
be a prime ideal in 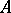 ; let
; let 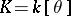 , where
, where 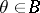 and the elements
and the elements 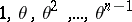 constitute a basis for the
constitute a basis for the 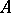 -module
-module  ; finally, let
; finally, let  be the irreducible polynomial of
be the irreducible polynomial of 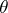 , let
, let 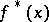 be the image of
be the image of 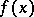 in the ring
in the ring 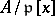 and let
and let 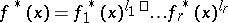 be the irreducible factorization of
be the irreducible factorization of 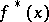 in
in 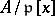 . Then the prime ideal factorization of the ideal
. Then the prime ideal factorization of the ideal  in
in 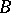 is
is
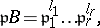 |
with the degree of the polynomial 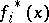 equal to the degree
equal to the degree  of the extension of the field of residues.
of the extension of the field of residues.
Kummer's theorem makes it possible to determine the factorization of a prime ideal over an extension of the ground field in terms of the factorization in the residue class field of the irreducible polynomial of a suitable primitive element of the extension.
The theorem was first proved, for certain particular cases, by E.E. Kummer [1]; he used it to determine the factorization law in cyclotomic fields and in certain cyclic extensions of cyclotomic fields (cf. Cyclotomic field).
References
| [1] | E.E. Kummer, "Zur Theorie der complexen Zahlen" J. Reine Angew. Math. , 35 (1847) pp. 319–326 |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Comments
References
| [a1] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) pp. Sects. 4–9 |
Kummer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kummer_theorem&oldid=35053