Functorial morphism

natural transformation

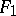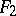An analogue of the concept of a homomorphism of (left) modules with common ring of scalars (in this, the role of the ring is played by the domain of definition of the functors, and the functors themselves play the role of the modules). Suppose that and are one-place covariant functors from a category 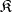into a category 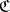. A functorial morphism 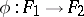associates to each object 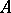of 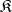a morphism 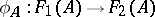, in such a way that for every morphism 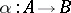in 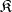the following diagram is commutative:

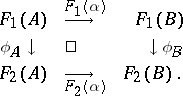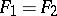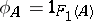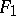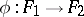If , then, setting , one obtains the so-called identity morphism of the functor . If and 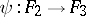are two functorial morphisms, then, setting 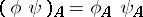, one obtains the functorial morphism 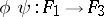, called the product of 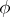and 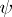. Composition of functorial morphisms is associative. Therefore, for a small category 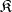, all functors from 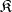into 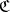and their functorial morphisms form a so-called functor category 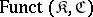, or a category of diagrams with scheme .

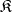Let 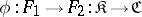be a functorial morphism and let 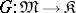and 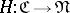be two functors. The formulas

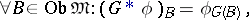define functorial morphisms 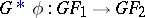and 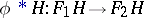, respectively. Then for any functorial morphisms 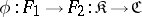and 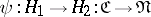, the following relationship holds:

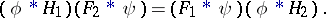A functorial morphism is also called a natural transformation of functors. Functorial morphisms of many-place functors are defined by analogy with functorial morphisms of one-place functors.

Comments

The term "natural transformation" is common.

References

[a1]	B. Mitchell, Theory of categories, Acad. Press (1965)
[a2]	Saunders Mac Lane, Categories for the Working Mathematician, Graduate Texts in Mathematics 5, Springer (1998) ISBN 0-387-98403-8