Parabolic partial differential equation
An equation (cf. Differential equation, partial) of the form
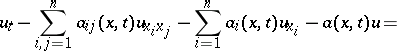 |
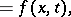 |
where  is a positive-definite quadratic form. The variable
is a positive-definite quadratic form. The variable  is singled out and plays the role of time. A typical example of a parabolic partial differential equation is the heat equation
is singled out and plays the role of time. A typical example of a parabolic partial differential equation is the heat equation
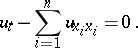 |
Comments
The above defines second-order linear parabolic differential equations. There also exist notions of non-linear parabolic equations. For instance, in [a2] equations are studied of the form  , where
, where  is a function of variables
is a function of variables  such that for a certain
such that for a certain  one has
one has 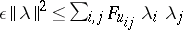 on the domain under consideration.
on the domain under consideration.
A semi-linear partial differential equation of the second order, i.e. one of the form  , is said to be of parabolic type if
, is said to be of parabolic type if  at each point of the domain under consideration.
at each point of the domain under consideration.
References
| [a1] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) MR0181836 Zbl 0144.34903 |
| [a2] | N.V. Krylov, "Nonlinear elliptic and parabolic equations of the second order" , Reidel (1987) (Translated from Russian) MR0901759 Zbl 0619.35004 |
Parabolic partial differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_partial_differential_equation&oldid=28257