Lipschitz condition
A restriction on the behaviour of increase of a function. If for any points  and
and 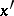 belonging to an interval
belonging to an interval 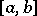 the increase of a function
the increase of a function 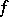 satisfies the inequality
satisfies the inequality
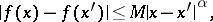 | (*) |
where 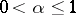 and
and 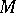 is a constant, then one says that
is a constant, then one says that 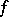 satisfies a Lipschitz condition of order
satisfies a Lipschitz condition of order 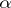 on
on 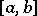 and writes
and writes 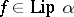 ,
, 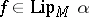 or
or 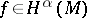 . Every function that satisfies a Lipschitz condition with some
. Every function that satisfies a Lipschitz condition with some 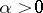 on
on 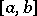 is uniformly continuous on
is uniformly continuous on 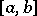 , and functions that satisfy a Lipschitz condition of order
, and functions that satisfy a Lipschitz condition of order 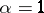 are absolutely continuous (cf. Absolute continuity; Uniform continuity). A function that has a bounded derivative on
are absolutely continuous (cf. Absolute continuity; Uniform continuity). A function that has a bounded derivative on 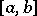 satisfies a Lipschitz condition on
satisfies a Lipschitz condition on  with any
with any 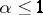 .
.
The Lipschitz condition (*) is equivalent to the condition
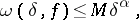 |
where 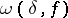 is the modulus of continuity (cf. Continuity, modulus of) of
is the modulus of continuity (cf. Continuity, modulus of) of 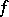 on
on 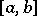 . Lipschitz conditions were first considered by R. Lipschitz [1] as a sufficient condition for the convergence of the Fourier series of
. Lipschitz conditions were first considered by R. Lipschitz [1] as a sufficient condition for the convergence of the Fourier series of 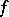 . In the case
. In the case 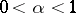 the condition (*) is also called a Hölder condition of order
the condition (*) is also called a Hölder condition of order 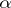 .
.
References
| [1] | R. Lipschitz, "De explicatione per series trigonometricas insttuenda functionum unius variablis arbitrariarum, et praecipue earum, quae per variablis spatium finitum valorum maximorum et minimorum numerum habent infintum disquisitio" J. Reine Angew. Math. , 63 (1864) pp. 296–308 |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) MR0933759 Zbl 0628.42001 |
| [3] | I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian) MR1868029 MR0196342 MR0196341 MR0196340 Zbl 1034.01022 Zbl 0178.39701 Zbl 0136.36302 Zbl 0133.31101 |
Lipschitz condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lipschitz_condition&oldid=28238