Harmonic polynomial

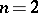A polynomial with as variables that satisfies the Laplace equation. Any harmonic polynomial may be represented as the sum of homogeneous harmonic polynomials. If , there are only two linearly independent homogeneous harmonic polynomials of degree 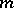— for example, the real and the imaginary part of the expression 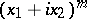. If 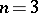, the number of linearly independent homogeneous polynomials of degree 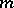is 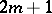. In the general case — 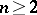— the number of linearly independent homogeneous harmonic polynomials of degree 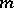is

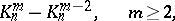where

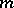is the number of permutations of objects taken at a time with 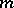repetitions. The homogeneous harmonic polynomials, 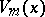, are also known as spherical functions (in particular 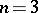if ). If , one may write, in spherical coordinates

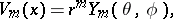where 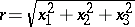and 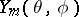is a spherical function of degree .

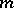References

[1]	S.L. Sobolev, "Partial differential equations of mathematical physics" , Pergamon (1964) (Translated from Russian) MR0178220 Zbl 0123.06508
[2]	A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) MR104888
[3]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) MR0106366 Zbl 0084.30903

E.D. Solomentsev

A finite linear combination of harmonics. Real-valued harmonic polynomials can be represented in the form

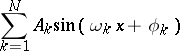for a given natural number 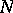, non-negative 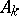, and real 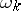, , 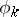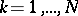. Complex-valued harmonic polynomials can be represented in the form

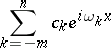where and 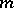are natural numbers, 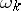is real and the 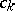, , 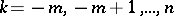are complex. Harmonic polynomials are the simplest almost-periodic functions (cf. Almost-periodic function).