Convolution of functions
 and
and 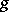 belonging to
belonging to 
The function  defined by
defined by
 |
it is denoted by the symbol  . The function
. The function  is defined almost everywhere and also belongs to
is defined almost everywhere and also belongs to  . The convolution has the basic properties of multiplication, namely,
. The convolution has the basic properties of multiplication, namely,
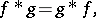 |
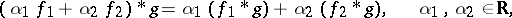 |
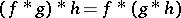 |
for any three functions in 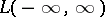 . Therefore,
. Therefore,  with the usual operations of addition and of multiplication by a scalar, with the operation of convolution as the multiplication of elements, and with the norm
with the usual operations of addition and of multiplication by a scalar, with the operation of convolution as the multiplication of elements, and with the norm
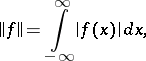 |
is a Banach algebra (for this norm  ). If
). If  denotes the Fourier transform of
denotes the Fourier transform of  , then
, then
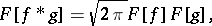 |
and this is used in solving a number of applied problems.
Thus, if a problem has been reduced to an integral equation of the form
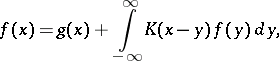 | (*) |
where
 |
 |
then, under the assumption that  , by applying the Fourier transformation to (*) one obtains
, by applying the Fourier transformation to (*) one obtains
 |
hence
 |
and the inverse Fourier transformation yields the solution to (*) as
 |
The properties of a convolution of functions have important applications in probability theory. If  and
and  are the probability densities of independent random variables
are the probability densities of independent random variables  and
and  , respectively, then
, respectively, then  is the probability density of the random variable
is the probability density of the random variable  .
.
The convolution operation can be extended to generalized functions (cf. Generalized function). If  and
and 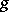 are generalized functions such that at least one of them has compact support, and if
are generalized functions such that at least one of them has compact support, and if  is a test function, then
is a test function, then  is defined by
is defined by
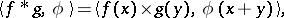 |
where  is the direct product of
is the direct product of 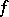 and
and  , that is, the functional on the space of test functions of two independent variables given by
, that is, the functional on the space of test functions of two independent variables given by
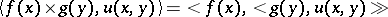 |
for every infinitely-differentiable function  of compact support.
of compact support.
The convolution of generalized functions also has the commutativity property and is linear in each argument; it is associative if at least two of the three generalized functions have compact supports. The following equalities hold:
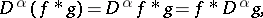 |
where  is the differentiation operator and
is the differentiation operator and  is any multi-index,
is any multi-index,
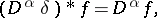 |
in particular, 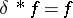 , where
, where  denotes the delta-function. Also, if
denotes the delta-function. Also, if 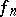 ,
, 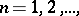 are generalized functions such that
are generalized functions such that 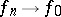 , and if there is a compact set
, and if there is a compact set 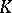 such that
such that
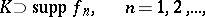 |
then
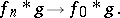 |
Finally, if 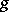 is a generalized function of compact support and
is a generalized function of compact support and  is a generalized function of slow growth, then the Fourier transformation can be applied to
is a generalized function of slow growth, then the Fourier transformation can be applied to  , and again
, and again
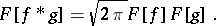 |
The convolution of generalized functions is widely used in solving boundary value problems for partial differential equations. Thus, the Poisson integral, written in the form
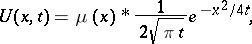 |
is a solution to the thermal-conductance equation for an infinite bar, where the initial temperature  can be not only an ordinary function but also a generalized one.
can be not only an ordinary function but also a generalized one.
Both for ordinary and generalized functions the concept of a convolution carries over in a natural way to functions of several variables; then in the above  and
and  must be regarded as vectors from
must be regarded as vectors from  and not as real numbers.
and not as real numbers.
References
| [1] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) MR0764399 Zbl 0954.35001 Zbl 0652.35002 Zbl 0695.35001 Zbl 0699.35005 Zbl 0607.35001 Zbl 0506.35001 Zbl 0223.35002 Zbl 0231.35002 Zbl 0207.09101 |
| [2] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 1–5 , Acad. Press (1964) (Translated from Russian) MR435831 Zbl 0115.33101 |
| [3] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) MR0942661 Zbl 0017.40404 Zbl 63.0367.05 |
Comments
References
| [a1] | W. Kecs, "The convolution product and some applications" , Reidel & Ed. Academici (1982) MR0690953 Zbl 0512.46041 |
Convolution of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convolution_of_functions&oldid=28165