Branching process with immigration

2020 Mathematics Subject Classification: Primary: 60J80 [MSN][ZBL]

A model of a branching process (discrete-time or continuous-time, with one or several types of particles, etc.) in which new particles may appear not only as the products of division of the original particles, but also as a result of immigration from some "external source" . For instance, let

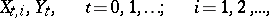be independent random variables with generating functions

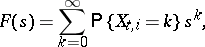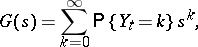respectively; the branching Galton–Watson process with immigration may be defined by the relations 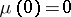, where 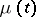is the number of particles and

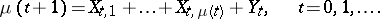Here, the variable 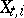is interpreted as the number of daughter particles of the 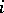-th particle of the 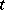-th generation, while the variable 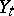is interpreted as the number of the particles which have immigrated into the 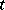-th generation. The generating functions

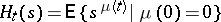are given by the recurrence relations

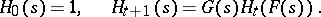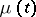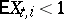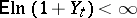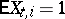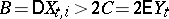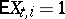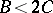The Markov chain corresponding to the Galton–Watson branching process with immigration is recurrent if and or and , and is transient if and or 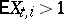. For the Markov chain 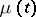to be ergodic, i.e. for the limits

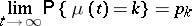to exist and to satisfy

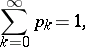it is necessary and sufficient [FW] that

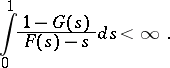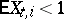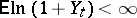This condition is met, in particular, if and . If 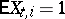, , 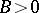, 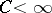then [S]

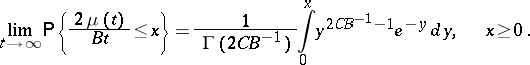If 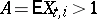and 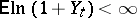, then there exists [S2] a sequence of numbers 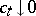, , 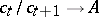such that

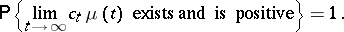In branching processes with immigration in which the immigration takes place at 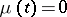only, i.e.

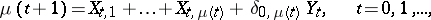where is the Kronecker symbol, the following relation is valid if 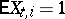, 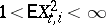and :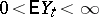

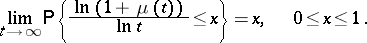References

[Z]	A.M. Zubkov, "Life-like periods of a branching process with immigration" Theory Probab. Appl. , 17 : 1 (1972) pp. 174–183 Teor. Veroyatnost. i Primenen. , 17 : 1 (1972) pp. 179–188 MR0300351 Zbl 0267.60084
[P]	A.G. Pakes, "Further results on the critical Galton–Watson process with immigration" J. Austral. Math. Soc. , 13 : 3 (1972) pp. 277–290 MR0312585 Zbl 0235.60078
[FW]	J.H. Foster, J.A. Williamson, "Limit theorems for the Galton–Watson process with time-dependent immigration" Z. Wahrsch. Verw. Geb. , 20 (1971) pp. 227–235 MR0305494 Zbl 0219.60069 Zbl 0212.19702
[S]	E. Seneta, "An explicit limit theorem for the critical Galton–Watson process with immigration" J. Roy. Statist. Soc. Ser. B , 32 : 1 (1970) pp. 149–152 MR0266320 Zbl 0198.52002
[S2]	E. Seneta, "On the supercritical Galton–Watson process with immigration" Math. Biosci. , 7 (1970) pp. 9–14 MR0270460 Zbl 0209.48804
[F]	J.H. Foster, "A limit theorem for a branching process with state-dependent immigration" Ann. of Math. Statist. , 42 : 5 (1971) pp. 1773–1776 MR0348854 Zbl 0245.60063

Comments

Additional references may be found in the article Branching process.