Bernoulli trials

2020 Mathematics Subject Classification: Primary: 60-01 [MSN][ZBL]

Independent trials, each one of which can have only two results ( "success" or "failure" ) such that the probabilities of the results do not change from one trial to another. Bernoulli trials are one of the principal schemes considered in probability theory.

Let be the probability of success, let be the probability of failure, and let 1 denote the occurrence of success, while 0 denotes the occurrence of a failure. The probability of a given sequence of successful or unsuccessful events, e.g.

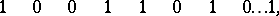is equal to

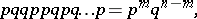where is the number of successful events in the series of trials under consideration. Many frequently occurring probability distributions are connected with Bernoulli trials. Let be the random variable which is equal to the number of successes in Bernoulli trials. The probability of the event is then

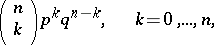i.e. 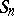has a binomial distribution. As , this distribution can be approximated by the normal distribution or by the Poisson distribution. Let be the number of trials prior to the first success. The probability of the event 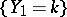then is

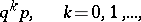i.e. 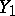has a geometric distribution. If 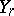is the number of failures which precede the -th appearance of a successful result, has the so-called negative binomial distribution. The number of successful outcomes of Bernoulli trials can be represented as the sum 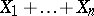of independent random variables, in which 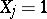if the 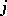-th trial was a success, and 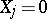otherwise. This is why many important laws of probability theory dealing with sums of independent variables were originally established for Bernoulli trial schemes (cf. Bernoulli theorem ((weak) Law of large numbers); Strong law of large numbers; Law of the iterated logarithm; Central limit theorem; etc.).

A rigorous study of infinite sequences of Bernoulli trials requires the introduction of a probability measure in the space of infinite sequences of zeros and ones. This may be done directly or by the method illustrated for the case below. Let 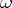be a number, uniformly distributed on the segment , and let

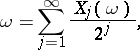where 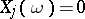or 1, be the expansion of 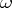into a binary fraction. Then the , are independent and assume the values 0 and 1 with probability each, i.e. the succession of zeros and ones in the expansion of is described by the Bernoulli trial scheme with 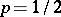. However, the measure on 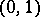can also be specified so as to obtain Bernoulli trials with any desired 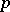(if 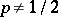the measure obtained is singular with respect to the Lebesgue measure).

Bernoulli trials are often treated geometrically (cf. Bernoulli random walk). Certain probabilities of a large number of events connected with Bernoulli trials were computed in the initial stage of development of probability theory in the context of the ruin problem.

References

[1]	B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian)
[2]	W. Feller, "An introduction to probability theory and its applications", Wiley (1957–1971)
[3]	M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) MR0110114 Zbl 0112.09101