Birkhoff ergodic theorem

2020 Mathematics Subject Classification: Primary: 37A30 Secondary: 37A0537A10 [MSN][ZBL]

One of the most important theorems in ergodic theory. For an endomorphism of a space with a -finite measure Birkhoff's ergodic theorem states that for any function the limit

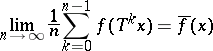(the time average or the average along a trajectory) exists almost everywhere (for almost all ). Moreover, , and if , then

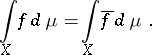For a measurable flow 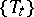in the space 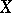with a 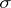-finite measure Birkhoff's ergodic theorem states that for any function 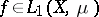the limit

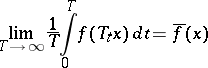exists almost everywhere, with the same properties of .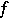

Birkhoff's theorem was stated and proved by G.D. Birkhoff [1]. It was then modified and generalized in various ways (there are theorems which contain, in addition to Birkhoff's theorem, also a number of statements of a somewhat different kind which are known in probability theory as ergodic theorems (cf. Ergodic theorem); there also exist ergodic theorems for more general semi-groups of transformations [2]). Birkhoff's ergodic theorem and its generalizations are known as individual ergodic theorems, since they deal with the existence of averages along almost each individual trajectory, as distinct from statistical ergodic theorems — the von Neumann ergodic theorem and its generalizations. (In non-Soviet literature the term "pointwise ergodic theorempointwise ergodic theorem" is often used to stress the fact that the averages are almost-everywhere convergent.)

References

[1]	G.D. Birkhoff, "Proof of the ergodic theorem" Proc. Nat. Acad. Sci. USA , 17 (1931) pp. 656–660 Zbl 0003.25602 Zbl 57.1011.02
[2]	A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 : 6 (1977) pp. 974–1065 Itogi Nauk. i Tekhn. Mat. Analiz , 13 (1975) pp. 129–262 MR0584389 Zbl 0399.28011

Comments

In non-Soviet literature, the term mean ergodic theorem is used instead of "statistical ergodic theorem" .

A comprehensive overview of ergodic theorems is in [a1]. Many books on ergodic theory contain full proofs of (one or more) ergodic theorems; see e.g. [a2].

References

[a1]	U. Krengel, "Ergodic theorems" , de Gruyter (1985) MR0797411 Zbl 0575.28009
[a2]	K. Peterson, "Ergodic theory" , Cambridge Univ. Press (1983) MR0833286 Zbl 0507.28010