Movable singular point

A singular point 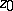of the solution 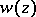of a differential equation 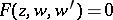( 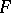is an analytic function), where 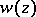is considered as a function of the complex variable , which is such that solutions to the same equation with initial data close to the original data have singular points close to but not coincident with it. The classical example of a movable singular point arises when considering the equation

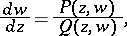where and 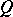are holomorphic functions in a certain region of the space 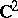. If the surface 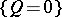is irreducible and is projected along the 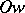-axis on a region 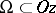, then all points in the region are movable singular points; for the solution with initial condition 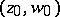, where

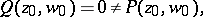the point 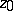is an algebraic branch point.

References

[1]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) MR0100119

Comments

For equations of the form

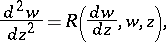where 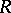is rational in 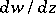and and analytic in , it is known which equations have only non-movable singularities, cf. Painlevé equation and [a1].

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) MR1570308 MR0010757 MR1524980 MR0000325 MR1522581 Zbl 0612.34002 Zbl 0191.09801 Zbl 0063.02971 Zbl 0022.13601 Zbl 65.1253.02 Zbl 53.0399.07