Limit cycle
A closed trajectory in the phase space of an autonomous system of ordinary differential equations that is an 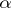 - or
- or 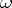 -limit set (cf. Limit set of a trajectory) of at least one other trajectory of this system. A limit cycle is called orbit stable, or stable, if for any
-limit set (cf. Limit set of a trajectory) of at least one other trajectory of this system. A limit cycle is called orbit stable, or stable, if for any 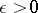 there is a
there is a 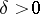 such that all trajectories starting in a
such that all trajectories starting in a 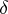 -neighbourhood of it for
-neighbourhood of it for 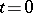 do not leave its
do not leave its  -neighbourhood for
-neighbourhood for  (cf. Orbit stability). A limit cycle corresponds to a periodic solution of the system, differing from a constant. In order for a periodic solution to correspond to a stable limit cycle it is sufficient that the moduli of all its multipliers, except one, be less than one (cf. Characteristic exponent; Andronov–Witt theorem). From the physical point of view, a limit cycle corresponds to periodic behaviour, or an auto-oscillation, of the system (cf. [2]).
(cf. Orbit stability). A limit cycle corresponds to a periodic solution of the system, differing from a constant. In order for a periodic solution to correspond to a stable limit cycle it is sufficient that the moduli of all its multipliers, except one, be less than one (cf. Characteristic exponent; Andronov–Witt theorem). From the physical point of view, a limit cycle corresponds to periodic behaviour, or an auto-oscillation, of the system (cf. [2]).
Suppose that an autonomous system
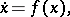 | (*) |
defined in a region 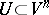 , where
, where 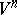 is a differentiable manifold, e.g.
is a differentiable manifold, e.g.  , has a closed trajectory
, has a closed trajectory 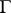 . Draw the hyperplane
. Draw the hyperplane 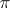 intersecting
intersecting 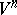 transversally at a point
transversally at a point 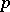 . Then every trajectory of the system starting for
. Then every trajectory of the system starting for 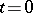 at a point
at a point 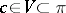 , with
, with 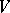 a sufficiently small neighbourhood of
a sufficiently small neighbourhood of 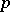 , intersects
, intersects 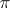 again, at a point
again, at a point 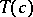 , as
, as 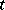 increases. The diffeomorphism
increases. The diffeomorphism 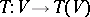 has fixed point
has fixed point 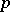 and is called the Poincaré return map. Its properties determine the behaviour of trajectories of the system in a neighbourhood of
and is called the Poincaré return map. Its properties determine the behaviour of trajectories of the system in a neighbourhood of  . A limit cycle, as distinct from an arbitrary closed trajectory, always determines a Poincaré return map that is not the identity. If
. A limit cycle, as distinct from an arbitrary closed trajectory, always determines a Poincaré return map that is not the identity. If  is a saddle point of the diffeomorphism
is a saddle point of the diffeomorphism 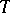 , then the limit cycle
, then the limit cycle 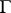 is said to be of saddle type. A system having a limit cycle of saddle type can have homoclinic curves, i.e. trajectories for which the limit cycle is both the
is said to be of saddle type. A system having a limit cycle of saddle type can have homoclinic curves, i.e. trajectories for which the limit cycle is both the 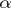 - and the
- and the 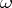 -limit set.
-limit set.
In the case of a two-dimensional system (*) 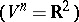 one takes a straight line for
one takes a straight line for 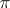 and considers the function
and considers the function 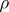 ,
, 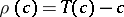 , which is called the Poincaré return function. The multiplicity of the zero
, which is called the Poincaré return function. The multiplicity of the zero 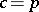 of
of 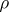 is called the multiplicity of the limit cycle. A limit cycle of even multiplicity is called semi-stable. The limit cycles, together with the rest points and the separatrices (cf. Separatrix), determine the qualitative picture of the behaviour of the other trajectories (cf. Poincaré–Bendixson theory, as well as [3], [4]). In the case of an analytic function
is called the multiplicity of the limit cycle. A limit cycle of even multiplicity is called semi-stable. The limit cycles, together with the rest points and the separatrices (cf. Separatrix), determine the qualitative picture of the behaviour of the other trajectories (cf. Poincaré–Bendixson theory, as well as [3], [4]). In the case of an analytic function 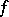 the limit cycles belong to one of the following three types: 1) stable; 2) unstable, i.e. stable if the direction of
the limit cycles belong to one of the following three types: 1) stable; 2) unstable, i.e. stable if the direction of 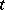 is reversed; or 3) semi-stable. E.g., the system
is reversed; or 3) semi-stable. E.g., the system
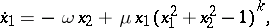 |
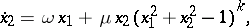 |
where 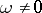 ,
, 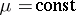 ,
, 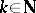 , has for
, has for  (
(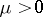 ) and
) and 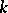 odd a stable (unstable) limit cycle of multiplicity
odd a stable (unstable) limit cycle of multiplicity 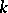 , while for
, while for 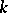 even it has a limit cycle of multiplicity
even it has a limit cycle of multiplicity 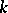 . In all cases the limit cycle is the circle
. In all cases the limit cycle is the circle 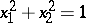 , i.e. the trajectory of the solution
, i.e. the trajectory of the solution
 |
If the system (*) is given on a simply-connected domain 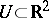 , then a limit cycle encircles at least one rest point of the system.
, then a limit cycle encircles at least one rest point of the system.
In order to find limit cycles of second-order systems one uses methods based on the following fact: If a vector field 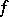 is directed inwards (outwards) an annular domain
is directed inwards (outwards) an annular domain 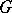 and if
and if 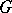 does not contain rest points, then there is at least one stable (unstable) limit cycle in
does not contain rest points, then there is at least one stable (unstable) limit cycle in 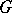 . The choice of
. The choice of 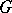 is based on physical considerations or results from analytic or numerical computations.
is based on physical considerations or results from analytic or numerical computations.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) MR0140742 Zbl 0112.05502 |
| [2] | A.A. Andronov, A.A. Vitt, A.E. Khaikin, "Theory of oscillators" , Dover, reprint (1987) (Translated from Russian) MR0925417 Zbl 0188.56304 |
| [3] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) MR0350126 Zbl 0282.34022 |
| [4] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamic systems on a plane" , Israel Program Sci. Transl. (1971) (Translated from Russian) MR0344606 |
| [5] | W.A. Pliss, "Nonlocal problems of the theory of oscillations" , Acad. Press (1966) (Translated from Russian) MR0196199 Zbl 0151.12104 |
| [6] | N.N. Moiseev, "Asymptotic methods of non-linear mechanics" , Moscow (1969) (In Russian) |
Comments
All definitions given above can be formulated for arbitrary dynamical systems, not necessarily defined by an autonomous system of ordinary differential equations. Most of the results are also meaningful in that case. For the Poincaré–Bendixson theory, see also e.g. [a1], Sect. VIII.1. A good additional general reference is [a2].
References
| [a1] | O. Hajek, "Dynamical systems in the plane" , Acad. Press (1968) MR0240418 Zbl 0169.54401 |
| [a2] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 MR0069338 Zbl 0064.33002 |
Limit cycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_cycle&oldid=24494