Multi-dimensional knot
An isotopy class of imbeddings of a sphere into a sphere. More precisely, an  -dimensional knot of codimension
-dimensional knot of codimension 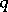 is a pair
is a pair 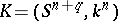 consisting of an oriented sphere
consisting of an oriented sphere  and an oriented, locally flat, submanifold of it,
and an oriented, locally flat, submanifold of it, 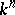 , homeomorphic to the sphere
, homeomorphic to the sphere 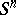 . Two knots
. Two knots 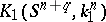 and
and  are called equivalent if there is an isotopy (in topology) of
are called equivalent if there is an isotopy (in topology) of 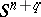 which takes
which takes 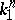 to
to 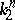 while preserving the orientation. Depending on the category (Diff, PL or Top) from which the terms "submanifold" and "isotopy" in these definitions are taken, one speaks of smooth, piecewise-linear or topological multi-dimensional knots, respectively. In the smooth case
while preserving the orientation. Depending on the category (Diff, PL or Top) from which the terms "submanifold" and "isotopy" in these definitions are taken, one speaks of smooth, piecewise-linear or topological multi-dimensional knots, respectively. In the smooth case 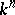 may have a non-standard differentiable structure. An
may have a non-standard differentiable structure. An  -dimensional knot of codimension
-dimensional knot of codimension 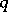 which is isotopic to the standard imbedding is called a trivial, or unknotted, knot.
which is isotopic to the standard imbedding is called a trivial, or unknotted, knot.
The study of multi-dimensional knots of codimension 1 is related to the Schoenflies conjecture. Every topological knot of codimension 1 is trivial. This is true for piecewise-linear and smooth knots if 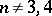 .
.
Piecewise-linear and topological multi-dimensional knots of codimension  are trivial. In the smooth case this is not so. The set of isotopy classes of smooth
are trivial. In the smooth case this is not so. The set of isotopy classes of smooth  -dimensional knots of codimension
-dimensional knots of codimension 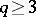 coincides, for
coincides, for 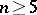 , with the set
, with the set 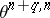 of cobordism classes of knots. (Two multi-dimensional knots
of cobordism classes of knots. (Two multi-dimensional knots 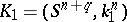 and
and 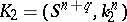 are called cobordant if there is a smooth
are called cobordant if there is a smooth 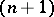 -dimensional submanifold
-dimensional submanifold 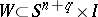 transversal to
transversal to 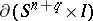 , where
, where  and
and 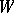 is an
is an 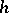 -cobordism between
-cobordism between 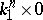 and
and  .) The set
.) The set 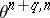 is an Abelian group with respect to the operation of connected sum. In this group the negative of the class of
is an Abelian group with respect to the operation of connected sum. In this group the negative of the class of  is the cobordism class of
is the cobordism class of 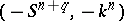 , where the minus denotes reversal of orientation. There is a natural homomorphism
, where the minus denotes reversal of orientation. There is a natural homomorphism 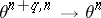 , where
, where 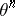 is the group of
is the group of  -dimensional homotopy spheres; this homomorphism associates the differentiable structure of
-dimensional homotopy spheres; this homomorphism associates the differentiable structure of 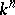 to the knot
to the knot 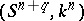 . The kernel of this homomorphism, denoted by
. The kernel of this homomorphism, denoted by 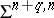 , is the set of isotopy classes of the standard sphere
, is the set of isotopy classes of the standard sphere 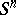 in
in 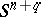 . If
. If 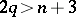 , then
, then 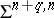 is trivial. If
is trivial. If  and
and 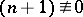 (
(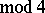 ), then
), then 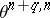 and
and 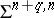 are finite. When
are finite. When  and
and 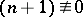 (
(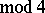 ), then
), then 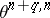 and
and 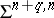 are finitely-generated Abelian groups of rank 1 (see [1], [2]). The set of concordance classes of smooth imbeddings of
are finitely-generated Abelian groups of rank 1 (see [1], [2]). The set of concordance classes of smooth imbeddings of 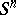 into
into 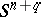 for
for 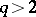 has also been calculated (see [3]).
has also been calculated (see [3]).
The study of multi-dimensional knots of codimension 2, which will subsequently simply be called knots, proceeds quite similarly in all three categories (Diff, PL, Top). For 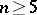 every topological knot may be transformed by an isotopy to a smooth knot. However, there are topological three-dimensional knots in
every topological knot may be transformed by an isotopy to a smooth knot. However, there are topological three-dimensional knots in 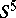 which are not equivalent, or even cobordant, to smooth knots (see [4]).
which are not equivalent, or even cobordant, to smooth knots (see [4]).
The set of isotopy classes of  -dimensional knots (in each category) is an Abelian semi-group with respect to the operation of connected sum. It is known that for
-dimensional knots (in each category) is an Abelian semi-group with respect to the operation of connected sum. It is known that for 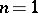 every element in this semi-group is a finite sum of primes, and such a decomposition is unique.
every element in this semi-group is a finite sum of primes, and such a decomposition is unique.
An  -dimensional knot
-dimensional knot  is trivial if and only if
is trivial if and only if 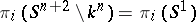 for all
for all 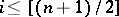 . An algebraic classification has been given (see [6]) of the knots
. An algebraic classification has been given (see [6]) of the knots 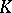 for which
for which 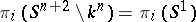 , for all
, for all 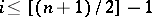 and
and  odd (knots of type
odd (knots of type 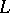 ): For
): For 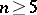 the set of isotopy classes of such knots turns out to be in one-to-one correspondence with the set of
the set of isotopy classes of such knots turns out to be in one-to-one correspondence with the set of 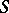 -equivalence classes of the Seifert matrix. Knots of type
-equivalence classes of the Seifert matrix. Knots of type 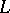 are important from the point of view of applications to algebraic geometry, since they contain all knots obtained by the following construction (see [15]). Let
are important from the point of view of applications to algebraic geometry, since they contain all knots obtained by the following construction (see [15]). Let 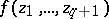 be a complex polynomial of non-zero degree having zero as an isolated singularity and let
be a complex polynomial of non-zero degree having zero as an isolated singularity and let 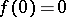 . The intersection
. The intersection 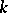 of the hyperplane
of the hyperplane  with a small sphere
with a small sphere 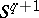 with centre at zero is a
with centre at zero is a 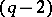 -connected
-connected 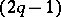 -dimensional manifold. The manifold
-dimensional manifold. The manifold 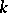 is homeomorphic to
is homeomorphic to 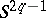 if and only if
if and only if 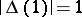 , where
, where 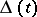 is the Alexander polynomial. In this case there thus arises a knot
is the Alexander polynomial. In this case there thus arises a knot 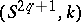 . Such knots are called algebraic; they are all of type
. Such knots are called algebraic; they are all of type 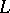 .
.
The exterior of a smooth knot  is the complement
is the complement 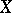 (of an open tubular neighbourhood) of
(of an open tubular neighbourhood) of 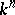 in
in 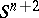 . For
. For 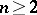 , for each
, for each  -dimensional knot
-dimensional knot 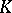 there is a knot
there is a knot 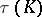 such that each knot with exterior diffeomorphic to the exterior of
such that each knot with exterior diffeomorphic to the exterior of 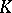 is equivalent to either
is equivalent to either 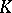 or
or 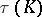 . If
. If 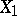 ,
, 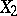 are the exteriors of two smooth
are the exteriors of two smooth  -dimensional knots,
-dimensional knots, 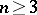 , and
, and 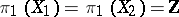 , then the following statements are equivalent (see [7]): 1)
, then the following statements are equivalent (see [7]): 1) 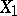 and
and 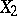 are diffeomorphic; and 2) the pairs
are diffeomorphic; and 2) the pairs 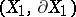 and
and 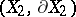 are homotopically equivalent. These results reduce the classification problem for knots to the homotopy classification of pairs
are homotopically equivalent. These results reduce the classification problem for knots to the homotopy classification of pairs 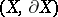 and the solution of the question: Does the exterior determine the type of a knot, that is, does
and the solution of the question: Does the exterior determine the type of a knot, that is, does 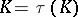 hold? It is known that this equality holds for knots of type
hold? It is known that this equality holds for knots of type 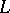 (see [6]) and for knots obtained by the Artin construction and the supertwisting construction (see [8]). However, two-dimensional knots have been found in
(see [6]) and for knots obtained by the Artin construction and the supertwisting construction (see [8]). However, two-dimensional knots have been found in 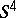 for which
for which  (see [9]).
(see [9]).
The study of the homotopy type of the exterior of 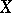 is complicated because this exterior is not simply connected. If
is complicated because this exterior is not simply connected. If 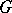 is the group of the knot (that is,
is the group of the knot (that is, 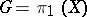 ), then
), then 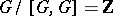 ,
, 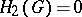 , and the weight of
, and the weight of 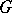 (that is, the minimal number of elements not contained in a proper normal divisor) is equal to 1. For
(that is, the minimal number of elements not contained in a proper normal divisor) is equal to 1. For 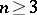 these properties completely describe the class of groups of
these properties completely describe the class of groups of  -dimensional knots (see [10]). The groups of one-dimensional and two-dimensional knots have a number of additional properties (see Knot theory; Two-dimensional knot).
-dimensional knots (see [10]). The groups of one-dimensional and two-dimensional knots have a number of additional properties (see Knot theory; Two-dimensional knot).
Since 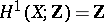 , the exterior
, the exterior 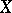 has a unique infinite cyclic covering
has a unique infinite cyclic covering 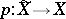 . The homology spaces
. The homology spaces 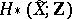 are
are 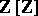 -modules. Their Alexander invariants are invariants of the knot. For algebraic properties of the modules
-modules. Their Alexander invariants are invariants of the knot. For algebraic properties of the modules  see [10]–[13].
see [10]–[13].
Due to the fact that the group 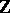 acts without fixed points on an infinite cyclic covering, the
acts without fixed points on an infinite cyclic covering, the 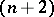 -dimensional non-compact manifold
-dimensional non-compact manifold  has a number of the homological properties of compact
has a number of the homological properties of compact 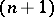 -dimensional manifolds. In particular, for the homology of the manifold
-dimensional manifolds. In particular, for the homology of the manifold 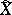 with coefficients from a field
with coefficients from a field 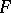 there is a non-degenerate pairing
there is a non-degenerate pairing
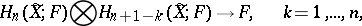 |
with properties resembling the pairing determined by the intersection index (in homology) in 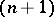 -dimensional compact manifolds. There is also a pairing
-dimensional compact manifolds. There is also a pairing
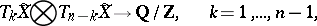 |
similar to the linking coefficients (cf. Linking coefficient) in 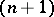 -dimensional manifolds (see [13]), where
-dimensional manifolds (see [13]), where  . These homology pairings generate invariants of the homotopy type of the pair
. These homology pairings generate invariants of the homotopy type of the pair 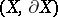 . To obtain algebraic invariants, finite-sheeted cyclic branched coverings are also used (see [14]).
. To obtain algebraic invariants, finite-sheeted cyclic branched coverings are also used (see [14]).
The problem of classifying knots of codimension 2 up to cobordism, a coarser equivalence relation than isotopy type, has been completely solved for 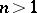 (see Cobordism of knots).
(see Cobordism of knots).
References
| [1] | A. Haefliger, "Knotted (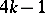 )-spheres in )-spheres in  -space" Ann. of Math. , 75 (1962) pp. 452–466 MR145539 -space" Ann. of Math. , 75 (1962) pp. 452–466 MR145539 |
| [2] | A. Haefliger, "Differentiable embeddings of 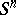 in in  for for 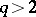 " Ann. of Math. , 83 (1966) pp. 402–436 Zbl 0151.32502 " Ann. of Math. , 83 (1966) pp. 402–436 Zbl 0151.32502 |
| [3] | J. Levine, "A classification of differentiable knots" Ann. of Math. , 82 (1965) pp. 15–50 MR0180981 Zbl 0136.21102 |
| [4] | S. Cappell, J. Shaneson, "Topological knots and knot cobordism" Topology , 12 (1973) pp. 33–40 MR0321099 Zbl 0268.57006 |
| [5] | A.B. Sossinskii, "Decomposition of knots" Math. USSR Sb. , 10 (1970) pp. 139–150 Mat. Sb. , 81 : 1 (1970) pp. 145–158 |
| [6] | J. Levine, "An algebraic classification of some knots of codimension two" Comment. Math. Helv. , 45 (1970) pp. 185–198 MR0266226 Zbl 0211.55902 |
| [7] | R. Lashof, J. Shaneson, "Classification of knots in codimension two" Bull. Amer. Math. Soc. , 75 (1969) pp. 171–175 MR0242175 Zbl 0198.28701 |
| [8] | S. Cappell, "Superspinning and knot complements" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1971) pp. 358–383 MR0276972 Zbl 0281.57001 |
| [9] | S. Cappell, J. Shaneson, "There exist inequivalent knots with the same complements" Ann. of Math. , 103 (1976) pp. 349–353 MR0413117 |
| [10] | M. Kervaire, "Les noeuds de dimensions supérieures" Bull. Soc. Math. France , 93 (1965) pp. 225–271 MR0189052 Zbl 0141.21201 |
| [11] | J. Levine, "Polynomial invariants of knots of codimension two" Ann. of Math. , 84 (1966) pp. 537–554 MR0200922 Zbl 0196.55905 |
| [12] | J. Levine, "Knot modules" , Knots, Groups and 3-Manifolds , Princeton Univ. Press (1975) pp. 25–34 MR0405437 Zbl 0336.57008 |
| [13] | M.Sh. Farber, "Duality in an infinite cyclic covering and even-dimensional knots" Math. USSR Izv. , 11 (1974) pp. 749–781 Izv. Akad. Nauk SSSR Ser. Mat. , 41 (1977) pp. 794–828 MR0515677 Zbl 0394.57011 |
| [14] | O.Ya. Viro, "Branched coverings of manifolds with boundary and link invariants I" Math. USSR Izv. , 7 (1973) pp. 1239–1256 Izv. Akad. Nauk SSSR Ser. Mat. , 37 (1973) pp. 1242–1258 Zbl 0295.55002 |
| [15] | J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) MR0239612 Zbl 0184.48405 |
Comments
References
| [a1] | J.W. Milnor, "Infinite cyclic coverings" J. Hocking (ed.) , Conf. Topology of Manifolds , Prindle, Weber & Schmidt (1968) pp. 115–133 MR0242163 Zbl 0179.52302 |
Multi-dimensional knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-dimensional_knot&oldid=23905