Arcsine distribution

2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]

A probability measure on the real line whose density is zero outside the interval and is if . The corresponding distribution function is equal to for .

The generalized arcsine distribution is employed together with the arcsine distribution. To the generalized arcsine distribution corresponds the distribution function with density

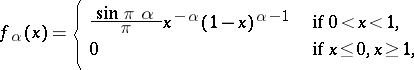if . The density coincides with the density of the arcsine distribution. The generalized arcsine distribution is a special case of the beta-distribution. The first-order moment of the generalized arcsine distribution is 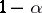, and its variance is 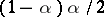. The arcsine distribution and the generalized arcsine distribution occur in the study of the fluctuations of random walks, in renewal theory (cf. Arcsine law), and are used in mathematical statistics as special cases of the beta-distribution.

References

[1]	W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971) MR0228020 MR0270403 Zbl 0598.60003 Zbl 0598.60002 Zbl 0219.60003 Zbl 0155.23101 Zbl 0158.34902 Zbl 0151.22403 Zbl 0138.10207 Zbl 0115.35308 Zbl 0077.12201 Zbl 0039.13201
[2]	M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" MR0246399, 3. Design and analysis MR0225406, Griffin (1969)