Wigner-Eckart theorem

A theorem describing the form of the matrix elements of tensor operators transforming under some representation of a group or a Lie algebra. Tensor operators are defined as follows. Let 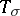be a finite-dimensional irreducible representation of a compact group 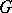acting on a linear space 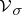with a basis 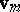, 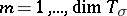. Let , , be a set of operators acting on a Hilbert space 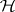. One says that the set 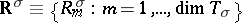is a tensor operator, transforming under the representation 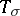of 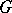, if there exists a representation 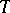(infinite dimensional if the space 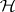is infinite dimensional) of 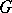on 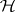such that for every element ,

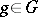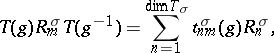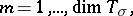where 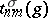are the matrix elements of the representation 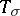with respect to the basis 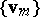. If the compact group 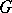is a Lie group, then the definition of tensor operator can be given also in infinitesimal form. Infinitesimal operators of representations of Lie algebras are important examples of tensor operators [a1].

In general, a representation 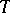of a group is reducible and decomposes into irreducible components: 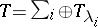. Let 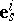, , 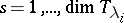be orthonormal bases in the support spaces of the representations .

The Wigner–Eckart theorem states that if no multiple irreducible representations appear, then the matrix elements 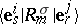of the operators 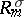with respect to the basis 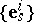of 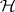are of the form

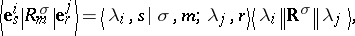where are the Clebsch–Gordan coefficients of the tensor product of the representations 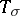and of (if multiple irreducible representations appear in these tensor products, then additional indices must be included) and 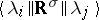are the so-called reduced matrix elements of the tensor operator 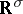. The reduced matrix elements are independent of indices of basis elements , , .

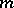The Wigner–Eckart theorem represents matrix elements of tensor operators as a product of two quantities: the first one (Clebsch–Gordan coefficient) is determined by a group structure and the second one (reduced matrix element) is independent of the group. The first quantity is the same for all tensor operators. Taking arbitrary numbers as reduced matrix elements one obtains, by the Wigner–Eckart theorem, matrix elements of some tensor operator, transforming under the representation .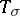

The Wigner–Eckart theorem can be formulated also for finite-dimensional and unitary infinite-dimensional representations of locally compact Lie groups, [a2]. The definition of tensor operators and the corresponding Wigner–Eckart theorem for quantum groups are more complicated.

The Wigner–Eckart theorem is a generalization of Schur's lemma on operators commuting with all representation operators (cf. Schur lemma). The Wigner–Eckart theorem and tensor operators are extensively used in quantum physics.

References

[a1]	L.C. Biedenharn, J.D. Louck, "Angular momentum in quantum physics" , Addison-Wesley (1981)
[a2]	A.U Klimyk, "Matrix elements and Clebsch-Gordan coefficients of group representations" , Naukova Dumka (1979) (In Russian)