Klein-Gordon equation
The relativistically-invariant quantum equation describing spinless scalar or pseudo-scalar particles, for example, 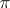 -, and
-, and 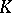 -mesons. The equation was established by O. Klein [1] and somewhat later by V.A. Fock [V.A. Fok] as a wave equation under the conditions of cyclicity in the fifth coordinate and was shortly afterwards deduced by several authors (for example, W. Gordon [2]) without this requirement on the fifth coordinate.
-mesons. The equation was established by O. Klein [1] and somewhat later by V.A. Fock [V.A. Fok] as a wave equation under the conditions of cyclicity in the fifth coordinate and was shortly afterwards deduced by several authors (for example, W. Gordon [2]) without this requirement on the fifth coordinate.
The subsequent application of the Klein–Gordon equation as a relativistic quantum equation proved possible in quantum field theory but not in quantum mechanics. In [3] an interpretation of the Klein–Gordon equation was given as an equation for fields of particles of zero spin. The Klein–Gordon equation is applied in the description of 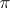 -mesons and corresponding fields; it plays the role of one of the fundamental equations of quantum field theory.
-mesons and corresponding fields; it plays the role of one of the fundamental equations of quantum field theory.
The Klein–Gordon equation is a linear homogeneous second-order partial differential equation with constant coefficients:
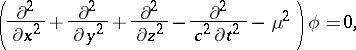 | (1) |
where  is a (pseudo-) scalar function, in the general case — complex,
is a (pseudo-) scalar function, in the general case — complex,  and
and 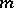 is the rest mass of the particle. If
is the rest mass of the particle. If 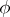 is a real function, then the Klein–Gordon equation describes neutral (pseudo-) scalar particles, while when
is a real function, then the Klein–Gordon equation describes neutral (pseudo-) scalar particles, while when 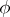 is complex it describes charged particles.
is complex it describes charged particles.
In the latter case equation (1) is supplemented by the equation for the complex-conjugate scalar function 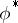 :
:
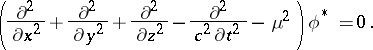 | (2) |
The interaction of (pseudo-) scalar particles with the electromagnetic field is described by the minimal substitution 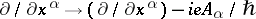 . Each component of the wave function of particles of any spin also satisfies the Klein–Gordon equation, but only for the case where the spin is 0 is the function invariant with respect to the Lorentz–Poincaré group.
. Each component of the wave function of particles of any spin also satisfies the Klein–Gordon equation, but only for the case where the spin is 0 is the function invariant with respect to the Lorentz–Poincaré group.
The Klein–Gordon equation can be obtained by means of the relationship between the energy 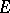 and the momentum
and the momentum 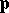 of the particle in special relativity theory,
of the particle in special relativity theory,
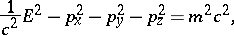 |
by replacing quantities by operators (see [4], [5]):
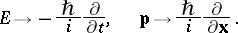 |
As for all relativistic equations, the Klein–Gordon equation can be expressed in the form of the Dirac equation, that is, it can be reduced to a first-order linear equation:
 | (3) |
where the coefficients 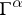 are matrices similar to the Dirac matrices
are matrices similar to the Dirac matrices 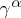 . In the case of the Klein–Gordon equation the matrices
. In the case of the Klein–Gordon equation the matrices 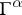 satisfy the commutation relations:
satisfy the commutation relations:
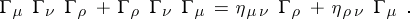 | (4) |
For example, 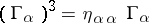 (Kemmer–Duffin matrices). Here
(Kemmer–Duffin matrices). Here 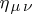 is the metric tensor of Minkowski space. All the
is the metric tensor of Minkowski space. All the 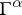 are singular matrices
are singular matrices 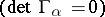 . Hence they do not have inverses.
. Hence they do not have inverses.
Apart from the trivial solution 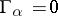 ,
,  to (4) and a solution in the form of five-row matrices, describing the scalar field
to (4) and a solution in the form of five-row matrices, describing the scalar field 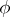 itself and the four components of its gradient, equation (4) has a further solution in the form of ten-row matrices. The corresponding ten-component function contains the four components of the potential
itself and the four components of its gradient, equation (4) has a further solution in the form of ten-row matrices. The corresponding ten-component function contains the four components of the potential 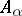 and the six components of the stress
and the six components of the stress 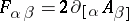 , that is, equations (3) and (4) can simultaneously give a representation for the Proca equation describing vector particles with spin 1; for
, that is, equations (3) and (4) can simultaneously give a representation for the Proca equation describing vector particles with spin 1; for 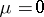 and real
and real 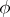 they give a representation of the Maxwell equations.
they give a representation of the Maxwell equations.
When taking into account the interaction of the (pseudo-) scalar particles with a gravity field in accordance with the general theory of relativity, the Klein–Gordon equation is generalized onto an arbitrary Riemannian space as:
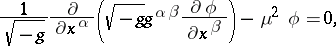 | (5) |
where 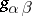 is the metric tensor and
is the metric tensor and 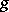 is the determinant of the matrix
is the determinant of the matrix 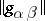 . In equation (5) the term
. In equation (5) the term 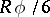 is frequently added, where
is frequently added, where 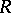 is the scalar curvature, as a result of which, when
is the scalar curvature, as a result of which, when 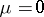 , the general relativistic Klein–Gordon equation
, the general relativistic Klein–Gordon equation
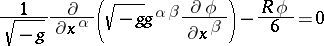 |
becomes conformally invariant.
References
| [1] | O. Klein, Z. Phys. , 37 (1926) pp. 895–906 |
| [2] | W. Gordon, Z. Phys. , 40 (1926–1927) pp. 117–133 |
| [3] | W. Pauli, V. Weisskopf, "Ueber die Quantisierung der skalaren relativistischen Wellengleichung" Helv. Phys. Acta , 7 (1934) pp. 709–731 |
| [4] | N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian) |
| [5] | S. Schweber, "An introduction to relativistic quantum field theory" , Harper & Row (1962) |
Comments
Explicit formulas for the fundamental solutions of the Klein–Gordon equation (1) are derived in [a1], [a2]. For a derivation of the commutation relations (4) see also [a3].
References
| [a1] | J. Hilgevoord, "Dispersion relations and causal description" , North-Holland (1960) |
| [a2] | E.M. de Jager, "The Lorentz-invariant solutions of the Klein–Gordon equation I-III" Indag. Math. , 25 : 4 (1963) pp. 515–531; 532–545; 546–558 |
| [a3] | P. Roman, "Theory of elementary particles" , North-Holland (1960) |
| [a4] | J.D. Björken, S.D. Drell, "Relativistic quantum mechanics" , McGraw-Hill (1964) |
Klein-Gordon equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Klein-Gordon_equation&oldid=22651