Kac-Moody algebra

Kac–Moody Lie algebra

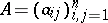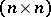Let be an -matrix satisfying conditions (see Cartan matrix)

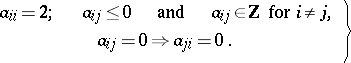(a1)

The associated Kac–Moody algebra 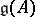is a Lie algebra over 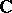on 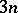generators 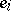, , 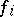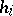(called the Chevalley generators) and the following defining relations:

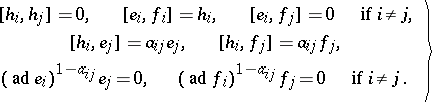(a2)

The Lie algebra 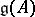is finite dimensional if and only if the matrix 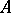is positive definite (i.e. all principal minors of 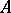are positive, cf. also Minor). One gets in this way all finite-dimensional semi-simple Lie algebras over 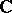(see Lie algebra, semi-simple). Thus, Kac–Moody algebras are infinite-dimensional analogues of the finite-dimensional semi-simple Lie algebras.

A systematic study of Kac–Moody algebras was started independently by V.G. Kac [a1] and R.V. Moody [a2], and subsequently many results of the theory of finite-dimensional semi-simple Lie algebras have been carried over to Kac–Moody algebras. The main technical tool of the theory is the generalized Casimir operator (cf. Casimir element), which can be constructed provided that the matrix 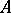is symmetrizable, i.e. 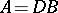for some invertible diagonal matrix 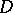and symmetric matrix 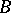[a3]. In the non-symmetrizable case more sophisticated geometric methods are required [a4], [a5].

One of the most important ingredients of the theory of Kac–Moody algebras are integrable highest-weight representations (cf. also Representation with a highest weight vector). Given an -tuple of non-negative integers 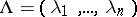, the integrable highest-weight representation 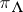of a Kac–Moody algebra 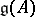is its irreducible representation on a complex vector space 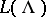, which is determined by the property that there exists a non-zero vector 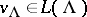such that

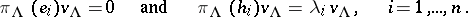Note that 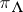are precisely all irreducible finite-dimensional representations of a finite-dimensional Kac–Moody algebra .

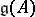The basic result of the theory of integrable highest-weight representations is the Weyl–Kac character formula [a3], which gives an explicit expression for the formal power series 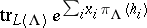in the 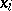in terms of 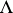(see also Character formula).

The numerous applications of Kac–Moody algebras are mainly related to the fact that the Kac–Moody algebras associated to positive semi-definite indecomposable Cartan matrices (called affine matrices) admit a very explicit construction. (A matrix is called indecomposable if it does not become block-diagonal after arbitrary permutation of the index set.) These Kac–Moody algebras are called affine algebras.

Below a construction of "non-twisted" affine algebras is given. Let 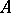be a positive-definite indecomposable Cartan matrix and let 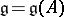be the associated simple finite-dimensional Lie algebra with Chevalley generators 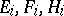, 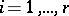. There exists a unique (up to a constant multiple) non-zero element 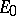(respectively, 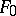) in 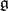such that 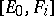(respectively, 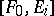) vanishes for 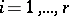. Then 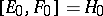, a linear combination of the 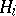(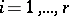), and one normalizes 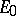and 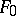by the conditions 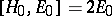, 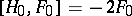. Then: 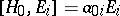, 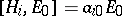for 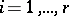, where the 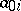are certain non-positive integers, and one puts

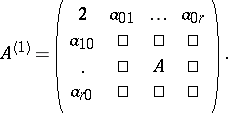This is a positive semi-definite 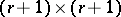matrix satisfying (a1) (called the extended Cartan matrix of 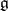). These matrices, along with all affine matrices, are listed in Lie algebra, graded. The associated affine algebra

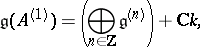where 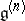is the -th copy of 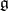and 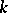is a central element (i.e. 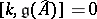), with the following commutation relations:

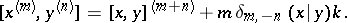Here 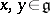, 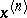denotes the element taken from 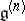and 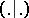is the Killing form on 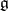normalized by the condition 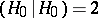. (Note that for 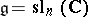, one has 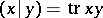.) The canonical generators of 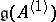are:

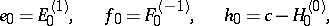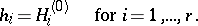In more geometric terms, 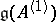is a central extension (by 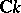) of the loop algebra, i.e. the Lie algebra of regular mappings of 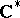to :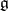

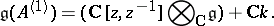This observation leads to geometric applications of affine algebras and the corresponding groups, called the loop groups (see [a6]).

In an integrable highest-weight representation 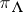, the central element 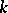acts as a non-negative integral scalar, also denoted by 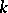, which is called the level of 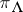. The only 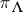of level is the trivial representation. A remarkable feature of the representation theory of the affine algebras is the existence of explicit canonical constructions for the 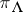of level 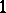. Below the simplest "vertex operator" construction for the basic representation 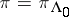, where 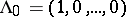, is explained. It uses the vertex operators, which are defined as follows. Let 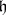be an -dimensional complex vector space with a symmetric bilinear form 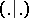and let 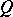be a lattice in 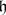of rank . For each 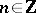, take a copy 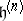of 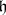and let 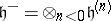. Let 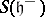be the symmetric algebra over 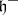and let 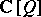be the group algebra of 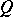with the inclusion 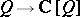denoted by 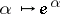. Consider the complex commutative associative algebra

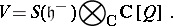For 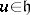and 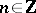define an operator 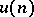on 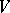as follows. For 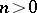, 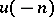is the operator of multiplication by 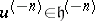; for 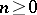, 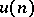is the derivation of 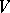defined by:

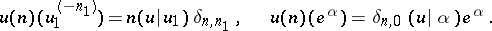For 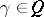such that 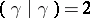, define the vertex operator

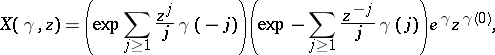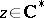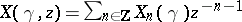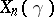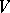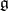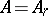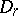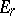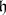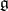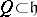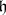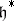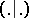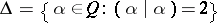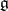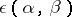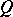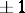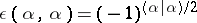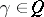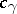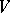where . Expanding in powers of : , one obtains a sequence of operators on . Let now be a simple Lie algebra with the Cartan matrix , or , choose a Cartan subalgebra of , let be the root lattice (identifying with using the form ), and let be the root system of . Choose a bimultiplicative function on with values such that . For , define an operator on by 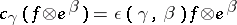. Then 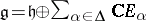with commutation relations:

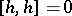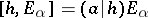; for ;

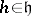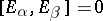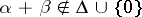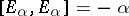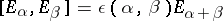if ;

; if .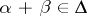

The basic representation of 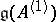is then defined on 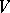by the following formulas [a11]:

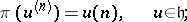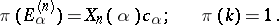This is called the homogeneous vertex operator construction of the basic representation.

The vertex operators were introduced in string theory around 1969, but the vertex operator construction entered string theory only at its revival in the mid 1980s. Thus, the representation theory of affine algebras became an important ingredient of string theory (see [a12]).

The vertex operators turned out to be useful even in the theory of finite simple groups. Namely, a twist of the homogeneous vertex operator construction based on the Leech lattice produced the 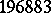-dimensional Griess algebra and its automorphism group, the famous finite simple Monster group (see Sporadic simple group) [a13].

The vertex operator constructions were, quite unexpectedly, applied to the theory of soliton equations. This was based on the observation (see [a14]) that the orbit of the vector 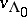of the basic representation under the loop group satisfies an infinite hierarchy of partial differential equations, the simplest of them being classical soliton equations, like the Korteweg–de Vries equation.

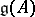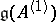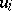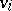The link of the representation theory of affine algebras to the conformal field theory is given by the Sugawara construction. Let be a simple finite-dimensional algebra and let be the corresponding affine algebra. Choose bases and of 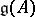such tha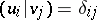t . Let

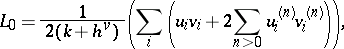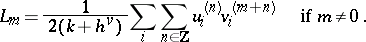Here 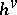is the dual Coxeter number (defined by: Killing form 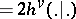). Then one has

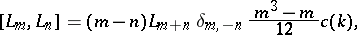where

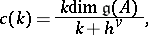producing thereby a representation of the Virasoro algebra.

The character of an integrable highest-weight representation 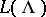of level 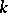of an affine algebra, multiplied by a suitable power of 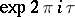, can be written in the following form:

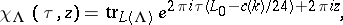where 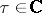and 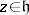. This is a series which converges for 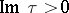to a modular function. Moreover, the linear span of the functions 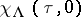for 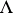of fixed level 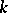is invariant under the modular transformations

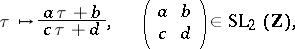and the matrix 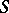of the transformation 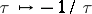is known explicitly [a7]. For example, in the case ,

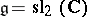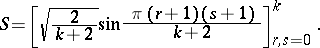This turned out to be a key fact in the representation theory of affine algebras, as well as its applications to conformal field theory (see [a8]), to -dimensional lattice models [a9], and even to knot theory [a10].

References

[a1]	V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 (1968) pp. 1271–1311 Izv. Akad. Nauk USSR Ser. Mat. , 32 (1968) pp. 1923–1967
[a2]	R.V. Moody, "A new class of Lie algebras" J. of Algebra , 10 (1968) pp. 211–230
[a3]	V.G. Kac, "Infinite-dimensional Lie algebras and Dedekind's 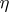-function" Funct. Anal. Appl. , 8 (1974) pp. 68–70 Funkts. Anal. i Prilozhen. , 8 : 1 (1974) pp. 77–78
[a4]	S. Kumar, "Demazure character formula in arbitrary Kac–Moody setting" Invent. Math. , 89 (1987) pp. 395–423
[a5]	O. Mathieu, "Formules de caractères pour les algèbres de Kac–Moody générales" Astérisque , 159–160 (1988) pp. 1–266
[a6]	A. Pressley, G. Segal, "Loop groups" , Oxford Univ. Press (1986)
[a7]	V.G. Kac, D.H. Peterson, "Infinite-dimensional Lie algebras, theta functions and modular forms" Adv. in Math. , 53 (1984) pp. 125–264
[a8]	E. Verlinde, "Fusion rules and modular transformations in 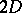conformal field theory" Nucl. Phys. , B300 pp. 360–375
[a9]	E. Date, M. Jimbo, A. Kuniba, T. Miwa, M. Okado, "Exactly solvable SOS models" Nucl. Phys. , B290 (1987) pp. 231–273
[a10]	C.N. Yang (ed.) M.L. Ge (ed.) , Braid group, knot theory and statistical mechanics , World Sci. (1989)
[a11]	I.B. Frenkel, V.G. Kac, "Basic representations of affine Lie algebras and dual resonance models" Invent. Math. , 62 (1980) pp. 23–66
[a12]	M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , Cambridge Univ. Press (1987)
[a13]	I. Frenkel, J. Lepowsky, A. Meurman, "Vertex operator algebras and the Monster" , Acad. Press (1989)
[a14]	E. Date, M. Jimbo, M. Kashiwara, T. Miwa, "Transformation groups for soliton equations" M. Jimbo (ed.) T. Miwa (ed.) , Proc. RIMS Symp. , World Sci. (1983) pp. 39–120
[a15]	V.G. Kac, "Infinite-dimensional Lie algebras" , Cambridge Univ. Press (1985)
[a16]	V.G. Kac, A.K. Raina, "Bombay lectures on highest weight representations" , World Sci. (1987)