Elliott-Daboussi theorem
The Delange theorem, proved in 1961, gives necessary and sufficient conditions for a multiplicative arithmetic function 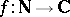 , of modulus
, of modulus 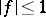 , to possess a non-zero mean value. The unpleasant condition
, to possess a non-zero mean value. The unpleasant condition 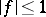 was replaced by P.D.T.A. Elliott, in 1975–1980, by boundedness of a semi-norm
was replaced by P.D.T.A. Elliott, in 1975–1980, by boundedness of a semi-norm
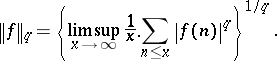 |
More precisely, Elliott showed (see [a4], [a6]) the following result. Assume that 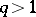 and that
and that 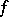 is a multiplicative arithmetic function with bounded semi-norm
is a multiplicative arithmetic function with bounded semi-norm 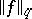 . Then the mean value
. Then the mean value
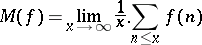 |
of 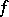 exists and is non-zero if and only if
exists and is non-zero if and only if
i) the four series
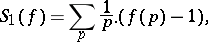 |
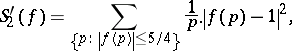 |
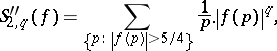 |
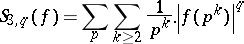 |
are convergent; and
ii) 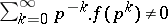 for every prime
for every prime 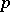 .
.
H. Daboussi [a3] gave another proof for this result and extended it [a2] to multiplicative functions 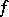 having at least one non-zero Fourier coefficient
having at least one non-zero Fourier coefficient 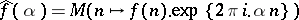 ; the necessary and sufficient conditions for this to happen are the convergence of the series
; the necessary and sufficient conditions for this to happen are the convergence of the series 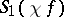 ,
, 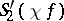 ,
, 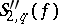 , and
, and 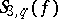 for some Dirichlet character
for some Dirichlet character 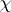 .
.
See also [a5], [a7], [a8], [a9], [a1]. In fact, the conditions of the Elliott–Daboussi theorem ensure that 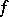 belongs to the space
belongs to the space 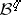 , which is the
, which is the 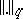 -closure of the vector space of linear combinations of the Ramanujan sums
-closure of the vector space of linear combinations of the Ramanujan sums 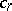 ,
, 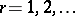 . For details see [a10], Chapts. VI, VII.
. For details see [a10], Chapts. VI, VII.
References
| [a1] | P. Codecà, M. Nair, "On Elliott's theorem on multiplicative functions" , Proc. Amalfi Conf. Analytic Number Theory , 1989 (1992) pp. 17–34 |
| [a2] | H. Daboussi, "Caractérisation des fonctions multiplicatives p.p. 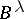 à spectre non vide" Ann. Inst. Fourier Grenoble , 30 (1980) pp. 141–166 à spectre non vide" Ann. Inst. Fourier Grenoble , 30 (1980) pp. 141–166 |
| [a3] | H. Daboussi, "Sur les fonctions multiplicatives ayant une valeur moyenne non nulle" Bull. Soc. Math. France , 109 (1981) pp. 183–205 |
| [a4] | P.D.T.A. Elliott, "A mean-value theorem for multiplicative functions" Proc. London Math. Soc. (3) , 31 (1975) pp. 418–438 |
| [a5] | P.D.T.A. Elliott, "Probabilistic number theory" , I–II , Springer (1979–1980) |
| [a6] | P.D.T.A. Elliott, "Mean value theorems for functions bounded in mean  -power, -power, 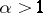 " J. Austral. Math. Soc. Ser. A , 29 (1980) pp. 177–205 " J. Austral. Math. Soc. Ser. A , 29 (1980) pp. 177–205 |
| [a7] | K.-H. Indlekofer, "A mean-value theorem for multiplicative functions" Math. Z. , 172 (1980) pp. 255–271 |
| [a8] | W. Schwarz, J. Spilker, "Eine Bemerkung zur Charakterisierung der fastperiodischen multiplikativen zahlentheoretischen Funktionen mit von Null verschiedenem Mittelwert" Analysis , 3 (1983) pp. 205–216 |
| [a9] | W. Schwarz, J. Spilker, "A variant of proof of Daboussi's theorem on the characterization of multiplicative functions with non-void Fourier–Bohr spectrum" Analysis , 6 (1986) pp. 237–249 |
| [a10] | W. Schwarz, J. Spilker, "Arithmetical functions" , Cambridge Univ. Press (1994) |
Elliott-Daboussi theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliott-Daboussi_theorem&oldid=22379