Drinfel'd-Turaev quantization

A type of quantization typically encountered in knot theory, for example in Jones–Conway, homotopy or Kauffman bracket skein modules of three-dimensional manifolds ([a3], [a1], [a2], cf. also Skein module).

Fix a commutative ring with identity, . Let be a Poisson algebra over and let be an algebra over which is free as an -module (cf. also Free module). An -module epimorphism is called a Drinfel'd–Turaev quantization of if

i) 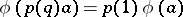for all and all ; and

ii) for all .

If is not required to be free as an -module, one obtains a so-called weak Drinfel'd–Turaev quantization.

References

[a1]	J. Hoste, J.H. Przytycki, "Homotopy skein modules of oriented -manifolds" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 475–488
[a2]	J.H. Przytycki, "Homotopy and -homotopy skein modules of -manifolds: An example in Algebra Situs" , Proc. Conf. in Low-Dimensional Topology in Honor of Joan Birman's 70th Birthday (Columbia Univ./Barnard College, March, 14-15, 1998) , Internat. Press (2000)
[a3]	V.G. Turaev, "Skein quantization of Poisson algebras of loops on surfaces" Ann. Sci. École Norm. Sup. , 4 : 24 (1991) pp. 635–704