Calderón couples
Let 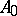 and
and 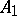 be two Banach spaces (cf. Banach space) embedded in a Hausdorff topological vector space. Such a pair of spaces is termed a Banach couple or Banach pair. The theory of interpolation of operators provides a variety of interpolation methods or interpolation functors for generating interpolation spaces with respect to any such couple
be two Banach spaces (cf. Banach space) embedded in a Hausdorff topological vector space. Such a pair of spaces is termed a Banach couple or Banach pair. The theory of interpolation of operators provides a variety of interpolation methods or interpolation functors for generating interpolation spaces with respect to any such couple 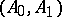 , namely normed spaces
, namely normed spaces 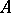 (cf. Normed space) having the property that every linear operator
(cf. Normed space) having the property that every linear operator 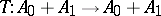 such that
such that 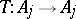 boundedly for
boundedly for 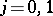 also maps
also maps 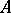 to
to  boundedly.
boundedly.
A fundamental problem in interpolation theory is the description of all interpolation spaces with respect to a given Banach pair  . In the 1960s, A.P. Calderón [a4] and B.S. Mityagin [a10] independently gave characterizations of all interpolation spaces
. In the 1960s, A.P. Calderón [a4] and B.S. Mityagin [a10] independently gave characterizations of all interpolation spaces 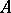 with respect to the particular couple
with respect to the particular couple 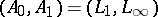 . Calderón showed that
. Calderón showed that 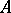 is an interpolation space if and only if it has the following monotonicity property: For every element
is an interpolation space if and only if it has the following monotonicity property: For every element  and every element
and every element 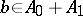 , whenever
, whenever 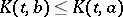 for all
for all  , it follows that
, it follows that 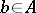 and
and 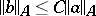 for some absolute constant
for some absolute constant 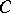 .
.
Here, 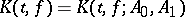 denotes the Peetre
denotes the Peetre  -functional of
-functional of  with respect to the couple
with respect to the couple 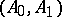 . In this particular case, where the couple is
. In this particular case, where the couple is 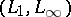 , there is a concrete formula for
, there is a concrete formula for 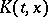 (cf. Interpolation of operators for further details).
(cf. Interpolation of operators for further details).
Mityagin's result, though of course ultimately equivalent to Calderón's, is formulated differently, in terms of the effect of measure-preserving transformations and multiplication by unimodular functions on elements of 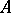 .
.
The work of Calderón and Mityagin triggered a long series of papers by many mathematicians (many of these are listed in [a2] and in [a5]) in which it was shown that all the interpolation spaces of many other Banach pairs 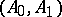 can also be characterized via the Peetre
can also be characterized via the Peetre 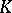 -functionals for those pairs, by a monotonicity condition exactly analogous to the one in Calderón's result above. The Banach pairs
-functionals for those pairs, by a monotonicity condition exactly analogous to the one in Calderón's result above. The Banach pairs 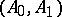 for which such a characterization holds are often referred to as Calderón couples or Calderón pairs. (They are also sometimes referred to using other terminology, such as Calderón–Mityagin couples,
for which such a characterization holds are often referred to as Calderón couples or Calderón pairs. (They are also sometimes referred to using other terminology, such as Calderón–Mityagin couples, 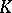 -monotone couples or
-monotone couples or 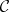 -pairs.)
-pairs.)
It is also convenient to use the terminology 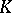 -space for any normed space
-space for any normed space 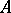 satisfying
satisfying 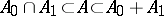 as well as the above-mentioned monotonicity property with respect to the
as well as the above-mentioned monotonicity property with respect to the 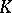 -functional for
-functional for 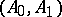 . By the important
. By the important 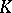 -divisibility theorem of Yu.A Brudnyi and N.Ya. Kruglyak [a2], it follows that each such
-divisibility theorem of Yu.A Brudnyi and N.Ya. Kruglyak [a2], it follows that each such 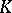 -space necessarily coincides, to within equivalence of norms, with a space of the special form
-space necessarily coincides, to within equivalence of norms, with a space of the special form 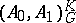 (as defined in Interpolation of operators). Thus, for Calderón pairs, all the interpolation spaces are of this relatively simple form.
(as defined in Interpolation of operators). Thus, for Calderón pairs, all the interpolation spaces are of this relatively simple form.
So, one can remark that, roughly speaking, for a Banach pair 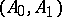 to be Calderón, the class of its interpolation spaces has to be relatively small, and correspondingly, the family of linear operators which are bounded on both
to be Calderón, the class of its interpolation spaces has to be relatively small, and correspondingly, the family of linear operators which are bounded on both 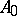 and
and 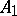 has to be relatively large.
has to be relatively large.
Those Banach pairs which are known to be Calderón include pairs 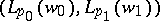 of weighted
of weighted 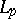 spaces for all choices of weight functions and for all exponents
spaces for all choices of weight functions and for all exponents 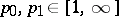 (the Sparr theorem, [a12]). Other examples include all Banach pairs of Hilbert spaces, various pairs of Hardy spaces, or of Lorentz or Marcinkiewicz spaces and all "iterated" pairs of the form
(the Sparr theorem, [a12]). Other examples include all Banach pairs of Hilbert spaces, various pairs of Hardy spaces, or of Lorentz or Marcinkiewicz spaces and all "iterated" pairs of the form
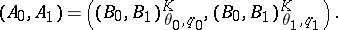 | (a1) |
In this last example 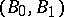 can be taken to be an arbitrary Banach pair and
can be taken to be an arbitrary Banach pair and 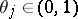 and
and 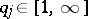 can be arbitrary numbers. Here,
can be arbitrary numbers. Here, 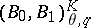 denotes the Lions–Peetre real-method interpolation space, consisting of all elements
denotes the Lions–Peetre real-method interpolation space, consisting of all elements 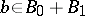 for which the norm
for which the norm
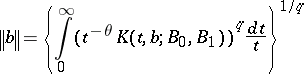 |
is finite.
By choosing particular pairs 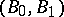 one obtains, as special cases of this last result, that various pairs of Besov spaces (cf. Imbedding theorems) or Lorentz
one obtains, as special cases of this last result, that various pairs of Besov spaces (cf. Imbedding theorems) or Lorentz 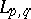 spaces or Schatten operator ideals are all Calderón.
spaces or Schatten operator ideals are all Calderón.
In parallel with all these positive results it has also been shown that many Banach pairs fail to be Calderón. These include 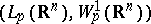 where
where 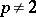 (here
(here 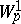 is a Sobolev space) and
is a Sobolev space) and 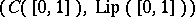 and also such simple pairs as
and also such simple pairs as 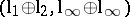 and
and 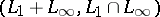 .
.
In [a3], Brudnyi and A. Shteinberg consider whether pairs of the form 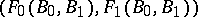 are Calderón, where
are Calderón, where 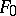 and
and 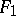 are interpolation functors (cf. Interpolation of operators). Their results for the pair
are interpolation functors (cf. Interpolation of operators). Their results for the pair  lead them to conjecture that the above-mentioned result about iterated pairs of the form (a1) cannot be extended, i.e., that
lead them to conjecture that the above-mentioned result about iterated pairs of the form (a1) cannot be extended, i.e., that 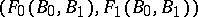 is Calderón for every Banach pair
is Calderón for every Banach pair  if and only if both functors
if and only if both functors 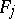 are of the form
are of the form 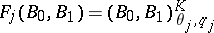 . As they also remark, all Calderón pairs which have so far (1996) been identified are either couples of Banach lattices of measurable functions on a given measure space, or are obtained from such lattice couples as partial retracts or
. As they also remark, all Calderón pairs which have so far (1996) been identified are either couples of Banach lattices of measurable functions on a given measure space, or are obtained from such lattice couples as partial retracts or 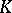 -subcouples. One can ask whether this might in fact be true for all Calderón pairs.
-subcouples. One can ask whether this might in fact be true for all Calderón pairs.
N.J. Kalton [a7] has given very extensive results about pairs of rearrangement-invariant spaces which are or are not Calderón, including a characterization of all rearrangement-invariant spaces  for which
for which 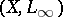 is Calderón. Kalton's results, and also the following general negative result from [a5], suggest that in some sense the Calderón property is very much linked to the spaces of the pair having some sort of
is Calderón. Kalton's results, and also the following general negative result from [a5], suggest that in some sense the Calderón property is very much linked to the spaces of the pair having some sort of 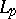 structure or "near-Lp" structure. This result also shows that Sparr's theorem for weighted
structure or "near-Lp" structure. This result also shows that Sparr's theorem for weighted 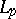 spaces cannot be sharpened: Let
spaces cannot be sharpened: Let 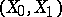 be a pair of saturated
be a pair of saturated 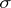 -order continuous Banach lattices with the Fatou property on the non-atomic measure space
-order continuous Banach lattices with the Fatou property on the non-atomic measure space 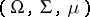 . Suppose that at least one of the spaces
. Suppose that at least one of the spaces 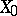 and
and 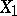 does not coincide, to within equivalence of norms, with a weighted
does not coincide, to within equivalence of norms, with a weighted 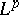 space on
space on  . Then there exist weight functions
. Then there exist weight functions  for
for 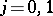 such that the weighted Banach pair
such that the weighted Banach pair 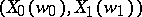 is not Calderón.
is not Calderón.
In most known examples of Banach pairs 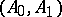 which are not Calderón, this happens because the complex interpolation spaces
which are not Calderón, this happens because the complex interpolation spaces 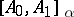 (see Interpolation of operators) are not
(see Interpolation of operators) are not 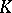 -spaces. But M. Mastyło and V.I. Ovchinnikov have found examples (see [a9]) of non-Calderón couples for which all the spaces
-spaces. But M. Mastyło and V.I. Ovchinnikov have found examples (see [a9]) of non-Calderón couples for which all the spaces 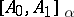 are
are 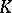 -spaces.
-spaces.
The notion of Calderón couples can also be considered in the wider context of operators  mapping from the spaces of one Banach pair
mapping from the spaces of one Banach pair  to a possibly different Banach pair
to a possibly different Banach pair 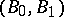 . In such a context one says that
. In such a context one says that 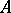 and
and  are relative interpolation spaces if every linear mapping
are relative interpolation spaces if every linear mapping 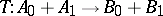 which maps
which maps 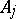 boundedly into
boundedly into 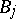 for
for  also maps
also maps 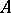 boundedly into
boundedly into 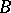 . (In the notation of Interpolation of operators,
. (In the notation of Interpolation of operators, 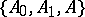 is an interpolation triple relative to
is an interpolation triple relative to 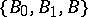 .) One says that
.) One says that 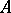 and
and 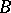 are relative
are relative 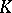 -spaces if, for all
-spaces if, for all 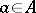 and
and 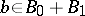 , the
, the 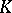 -functional inequality
-functional inequality
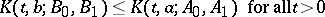 |
implies that 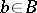 with
with 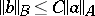 .
.
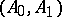 and
and 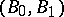 are said to be relative Calderón couples if
are said to be relative Calderón couples if 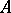 and
and  are relative interpolation spaces if and only if they are relative
are relative interpolation spaces if and only if they are relative 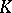 -spaces. J. Peetre has shown (see [a6]) that if
-spaces. J. Peetre has shown (see [a6]) that if 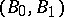 is any pair of weighted
is any pair of weighted 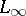 spaces, then
spaces, then 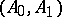 and
and 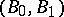 are relative Calderón couples for all Banach pairs
are relative Calderón couples for all Banach pairs 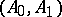 . Dually, if
. Dually, if 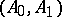 is an arbitrary pair of weighted
is an arbitrary pair of weighted 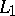 spaces, then
spaces, then 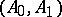 and
and 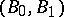 are relative Calderón couples for all Banach pairs
are relative Calderón couples for all Banach pairs 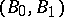 satisfying a mild "closure" condition. This latter result is another consequence of the Brudnyi–Kruglyak
satisfying a mild "closure" condition. This latter result is another consequence of the Brudnyi–Kruglyak 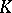 -divisibility theorem.
-divisibility theorem.
Finally, given that there are so many cases of couples whose interpolation spaces cannot be all characterized by a Calderón-style condition, one must also seek alternative ways to characterize interpolation spaces. See [a11] and [a8] for some special cases. (Cf. also [a1].)
References
| [a1] | J. Arazy, M. Cwikel, "A new characterization of the interpolation spaces between  and and 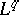 " Math. Scand. , 55 (1984) pp. 253–270 " Math. Scand. , 55 (1984) pp. 253–270 |
| [a2] | Y.A. Brudnyi, N.Ja. Krugljak, "Real interpolation functors" , North-Holland (1991) |
| [a3] | Y. Brudnyi, A. Shteinberg, "Calderón couples of Lipschitz spaces" J. Funct. Anal. , 131 (1995) pp. 459–498 |
| [a4] | A.P. Calderón, "Spaces between 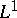 and and 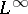 and the theorem of Marcinkiewicz" Studia Math. , 26 (1966) pp. 273–299 and the theorem of Marcinkiewicz" Studia Math. , 26 (1966) pp. 273–299 |
| [a5] | M. Cwikel, P. Nilsson, "Interpolation of weighted Banach lattices" , Memoirs , Amer. Math. Soc. (to appear) |
| [a6] | M. Cwikel, J. Peetre, "Abstract 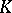 and and 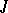 spaces" J. Math. Pures Appl. , 60 (1981) pp. 1–50 spaces" J. Math. Pures Appl. , 60 (1981) pp. 1–50 |
| [a7] | N.J. Kalton, "Calderón couples of re-arrangement invariant spaces" Studia Math. , 106 (1993) pp. 233–277 |
| [a8] | L. Maligranda, V.I. Ovchinnikov, "On interpolation between  and and  " J. Funct. Anal. , 107 (1992) pp. 343–351 " J. Funct. Anal. , 107 (1992) pp. 343–351 |
| [a9] | M. Mastyło, V.I. Ovchinnikov, "On the relation between complex and real methods of interpolation" Studia Math. (to appear) (Preprint Report 056/1996, Dept. Math. Comput. Sci. Adam Mickiewicz Univ., Poznan, 1996) |
| [a10] | B.S. Mityagin, "An interpolation theorem for modular spaces" , Proc. Conf. Interpolation Spaces and Allied Topics in Analysis, Lund, 1983 , Lecture Notes in Mathematics , 1070 , Springer (1984) pp. 10–23 (In Russian) Mat. Sbornik , 66 (1965) pp. 472–482 |
| [a11] | V.I. Ovchinnikov, "On the description of interpolation orbits in couples of 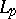 spaces when they are not described by the spaces when they are not described by the 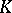 -method. Interpolation spaces and related topics" , Israel Math. Conf. Proc. Bar Ilan University , 5 , Amer. Math. Soc. (1992) pp. 187–206 -method. Interpolation spaces and related topics" , Israel Math. Conf. Proc. Bar Ilan University , 5 , Amer. Math. Soc. (1992) pp. 187–206 |
| [a12] | G. Sparr, "Interpolation of weighted 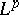 spaces" Studia Math. , 62 (1978) pp. 229–271 spaces" Studia Math. , 62 (1978) pp. 229–271 |
Calderón couples. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calder%C3%B3n_couples&oldid=22225