Hopf algebra
bi-algebra, hyperalgebra
A graded module 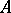 over an associative-commutative ring
over an associative-commutative ring 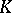 with identity, equipped simultaneously with the structure of an associative graded algebra
with identity, equipped simultaneously with the structure of an associative graded algebra 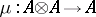 with identity (unit element)
with identity (unit element)  and the structure of an associative graded co-algebra
and the structure of an associative graded co-algebra 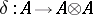 with co-identity (co-unit)
with co-identity (co-unit)  , satisfying the following conditions:
, satisfying the following conditions:
1)  is a homomorphism of graded co-algebras;
is a homomorphism of graded co-algebras;
2)  is a homomorphism of graded algebras;
is a homomorphism of graded algebras;
3) 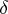 is a homomorphism of graded algebras.
is a homomorphism of graded algebras.
Condition 3) is equivalent to:
3') 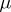 is a homomorphism of graded co-algebras.
is a homomorphism of graded co-algebras.
Sometimes the requirement that the co-multiplication is associative is discarded; such algebras are called quasi-Hopf algebras.
For any two Hopf algebras 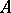 and
and 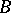 over
over 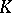 their tensor product
their tensor product 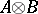 is endowed with the natural structure of a Hopf algebra. Let
is endowed with the natural structure of a Hopf algebra. Let  be a Hopf algebra, where all the
be a Hopf algebra, where all the 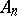 are finitely-generated projective
are finitely-generated projective 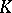 -modules. Then
-modules. Then 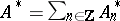 , where
, where 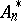 is the module dual to
is the module dual to 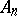 , endowed with the homomorphisms of graded modules
, endowed with the homomorphisms of graded modules  ,
, 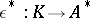 ,
, 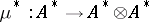 ,
,  , is a Hopf algebra; it is said to be dual to
, is a Hopf algebra; it is said to be dual to 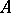 . An element
. An element  of a Hopf algebra
of a Hopf algebra 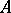 is called primitive if
is called primitive if
 |
The primitive elements form a graded subalgebra 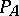 in
in 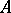 under the operation
under the operation
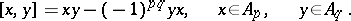 |
If 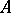 is connected (that is,
is connected (that is, 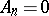 for
for 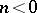 ,
, 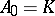 ) and if
) and if  is a field of characteristic 0, then the subspace
is a field of characteristic 0, then the subspace 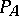 generates the algebra
generates the algebra 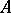 (with respect to multiplication) if and only if the co-multiplication is graded commutative [2].
(with respect to multiplication) if and only if the co-multiplication is graded commutative [2].
Examples.
1) For any graded Lie algebra  (that is, a graded algebra that is a Lie superalgebra under the natural
(that is, a graded algebra that is a Lie superalgebra under the natural 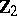 -grading) the universal enveloping algebra
-grading) the universal enveloping algebra 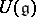 becomes a Hopf algebra if one puts
becomes a Hopf algebra if one puts
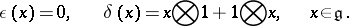 |
Here 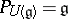 . If
. If  is a field of characteristic 0, then any connected Hopf algebra
is a field of characteristic 0, then any connected Hopf algebra  generated by primitive elements is naturally isomorphic to
generated by primitive elements is naturally isomorphic to 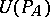 (see [2]).
(see [2]).
2) Similarly, the structure of a Hopf algebra (with a trivial grading) is defined in the group algebra 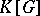 of an arbitrary group
of an arbitrary group 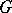 .
.
3) The algebra of regular functions on an affine algebraic group 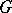 becomes a Hopf algebra (with trivial grading) if one defines the homomorphisms
becomes a Hopf algebra (with trivial grading) if one defines the homomorphisms 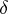 and
and  by means of the multiplication
by means of the multiplication 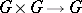 and the imbedding
and the imbedding 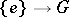 , where
, where  is the unit element of
is the unit element of  (see [3]).
(see [3]).
4) Suppose that  is a path-connected
is a path-connected 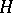 -space with multiplication
-space with multiplication 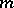 and unit element
and unit element  and suppose that
and suppose that 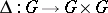 ,
, 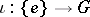 ,
, 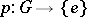 are defined by the formulas
are defined by the formulas  ,
, 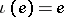 ,
, 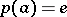 ,
, 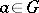 . If all cohomology modules
. If all cohomology modules 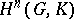 are projective and finitely generated, then the mappings
are projective and finitely generated, then the mappings  ,
, 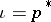 ,
, 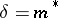 ,
,  induced in the cohomology, turn
induced in the cohomology, turn 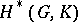 into a graded commutative quasi-Hopf algebra. If the multiplication
into a graded commutative quasi-Hopf algebra. If the multiplication 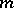 is homotopy-associative, then
is homotopy-associative, then  is a Hopf algebra, and the Hopf algebra dual to it is the homology algebra
is a Hopf algebra, and the Hopf algebra dual to it is the homology algebra 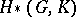 , equipped with the mappings
, equipped with the mappings 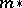 ,
, 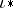 ,
,  ,
, 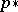 (the Pontryagin algebra). If
(the Pontryagin algebra). If 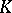 is a field of characteristic 0, then the Pontryagin algebra is generated by primitive elements and is isomorphic to
is a field of characteristic 0, then the Pontryagin algebra is generated by primitive elements and is isomorphic to 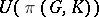 , where
, where 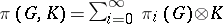 is regarded as a graded Lie algebra under the Samelson product (see [2]).
is regarded as a graded Lie algebra under the Samelson product (see [2]).
The algebra 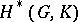 in Example 4) was first considered by H. Hopf in [1], who showed that it is an exterior algebra with generators of odd degrees if
in Example 4) was first considered by H. Hopf in [1], who showed that it is an exterior algebra with generators of odd degrees if  is a field of characteristic 0 and
is a field of characteristic 0 and 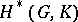 is finite-dimensional. The structure of an arbitrary connected, graded, commutative quasi-Hopf algebra
is finite-dimensional. The structure of an arbitrary connected, graded, commutative quasi-Hopf algebra  subject to the condition
subject to the condition 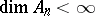 ,
, 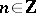 , over a perfect field
, over a perfect field 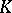 of characteristic
of characteristic 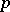 is described by the following theorem (see [4]). The algebra
is described by the following theorem (see [4]). The algebra 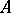 splits into the tensor product of algebras with a single generator
splits into the tensor product of algebras with a single generator  and the relation
and the relation 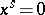 , where for
, where for 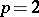 ,
,  is a power of 2 or
is a power of 2 or  , and for
, and for 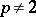 ,
,  is a power of
is a power of 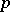 or
or 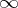 (
(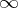 for
for 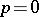 ) if
) if  has even degree, and
has even degree, and 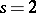 if the degree of
if the degree of  is odd. In particular, for
is odd. In particular, for 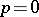 ,
, 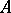 is the tensor product of an exterior algebra with generators of odd degree and an algebra of polynomials with generators of even degrees. On the other hand, every connected Hopf algebra
is the tensor product of an exterior algebra with generators of odd degree and an algebra of polynomials with generators of even degrees. On the other hand, every connected Hopf algebra 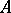 over a field
over a field 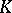 in which
in which 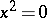 for any element
for any element  of odd degree and in which all elements of odd degree and all elements of even degree are decomposable, is the exterior algebra
of odd degree and in which all elements of odd degree and all elements of even degree are decomposable, is the exterior algebra 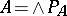 (see [2]). In particular, such are the cohomology algebra and the Pontryagin algebra of a connected compact Lie group over
(see [2]). In particular, such are the cohomology algebra and the Pontryagin algebra of a connected compact Lie group over 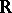 .
.
References
| [1] | H. Hopf, "Ueber die Topologie der Gruppenmannigfaltigkeiten und ihrer Verallgemeinerungen" Ann. of Math. (2) , 42 (1941) pp. 22–52 |
| [2] | J.W. Milnor, J.C. Moore, "On the structure of Hopf algebras" Ann. of Math. (2) , 81 : 2 (1965) pp. 211–264 MR0174052 Zbl 0163.28202 |
| [3] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [4] | A. Borel, "Sur la cohomologie des espaces fibrés principaux et des espaces homogènes de groupes de Lie compacts" Ann. of Math. , 57 (1953) pp. 115–207 MR0051508 Zbl 0052.40001 |
| [5] | S. MacLane, "Homology" , Springer (1963) Zbl 0818.18001 Zbl 0328.18009 |
Comments
Terminology concerning Hopf algebras and bi-algebras is not yet quite standardized. However, the following nomenclature (and notation) seems to be on the way of being universally accepted.
A bi-algebra is a module 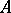 over
over 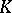 equipped with module mappings
equipped with module mappings 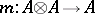 ,
, 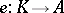 ,
,  ,
,  such that
such that
i)  is an associative algebra with unit;
is an associative algebra with unit;
ii) 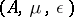 is a co-associative co-algebra with co-unit;
is a co-associative co-algebra with co-unit;
iii)  is a homomorphism of co-algebras;
is a homomorphism of co-algebras;
iv)  is a homomorphism of algebras;
is a homomorphism of algebras;
v) 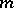 is a homomorphism of co-algebras.
is a homomorphism of co-algebras.
This last condition is equivalent to:
v') 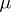 is a homomorphism of algebras.
is a homomorphism of algebras.
A grading is not assumed to be part of the definition. If there is a grading and every morphism under consideration is graded, then one speaks of a graded bi-algebra.
Let 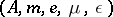 be a bi-algebra over
be a bi-algebra over 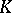 . An antipode for the bi-algebra is a module homomorphism
. An antipode for the bi-algebra is a module homomorphism  such that
such that
vi) 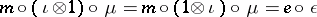 .
.
A bi-algebra with antipode  is called a Hopf algebra. A graded Hopf algebra is a graded bi-algebra with antipode
is called a Hopf algebra. A graded Hopf algebra is a graded bi-algebra with antipode  which is a homomorphism of graded modules.
which is a homomorphism of graded modules.
Given a co-algebra 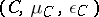 and an algebra
and an algebra 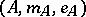 , the module
, the module 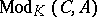 admits a convolution product, defined as follows
admits a convolution product, defined as follows
 |
In terms of this convolution product conditions vi) can be stated as
vi') 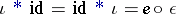 ,
,
where 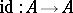 is the identity morphism of the bi-algebra
is the identity morphism of the bi-algebra 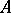 .
.
An additional example of a Hopf algebra is the following. Let 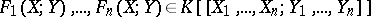 be a formal group. Let
be a formal group. Let 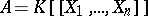 . Identifying
. Identifying 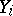 with
with 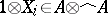 , the
, the 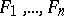 define a (continuous) algebra morphism
define a (continuous) algebra morphism 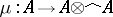 turning
turning 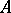 into a bi-algebra. There is an antipode making
into a bi-algebra. There is an antipode making 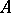 a Hopf algebra. It is called the contravariant bi-algebra or contravariant Hopf algebra of the formal group
a Hopf algebra. It is called the contravariant bi-algebra or contravariant Hopf algebra of the formal group 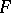 . Note that here the completed tensor product is used.
. Note that here the completed tensor product is used.
Hopf algebras, under the name quantum groups, and related objects have also become important in physics; in particular in connection with the quantum inverse-scattering method [a3], [a4].
References
| [a1] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977) MR1857062 MR0594432 MR0321962 Zbl 0476.16008 Zbl 0236.14021 |
| [a2] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) MR0506881 MR0463184 Zbl 0454.14020 |
| [a3] | V.G. Drinfel'd, "Quantum groups" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 798–820 |
| [a4] | L.D. Faddeev, "Integrable models in (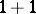 )-dimensional quantum field theory (Les Houches, 1982)" , Elsevier (1984) MR782509 )-dimensional quantum field theory (Les Houches, 1982)" , Elsevier (1984) MR782509 |
Hopf algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_algebra&oldid=21875