Markov moment
Markov time; stopping time
2020 Mathematics Subject Classification: Primary: 60G40 [MSN][ZBL]
A notion used in probability theory for random variables having the property of independence of the "future" . More precisely, let  be a measurable space with a non-decreasing family
be a measurable space with a non-decreasing family 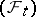 ,
, 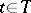 , of
, of 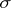 -algebras of
-algebras of 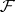 (
(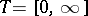 in the case of continuous time and
in the case of continuous time and 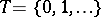 in the case of discrete time). A random variable
in the case of discrete time). A random variable 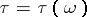 with values in
with values in 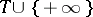 is called a Markov moment or Markov time (relative to the family
is called a Markov moment or Markov time (relative to the family 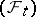 ,
, 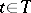 ) if for each
) if for each 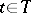 the event
the event 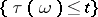 belongs to
belongs to 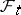 . In the case of discrete time this is equivalent to saying that for any
. In the case of discrete time this is equivalent to saying that for any 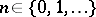 the event
the event 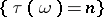 belongs to
belongs to 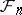 .
.
Examples.
1) Let 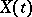 ,
, 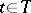 , be a real-valued right-continuous random process given on
, be a real-valued right-continuous random process given on 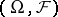 , and let
, and let 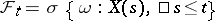 . Then the random variables
. Then the random variables
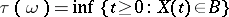 |
and
 |
that is, the (first and first after 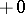 ) times of hitting the (Borel) set
) times of hitting the (Borel) set 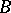 , form Markov moments (in the case
, form Markov moments (in the case 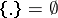 it is assumed that
it is assumed that 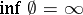 ).
).
2) If  ,
, 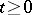 , is a standard Wiener process, then the Markov moment
, is a standard Wiener process, then the Markov moment
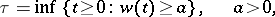 |
has probability density
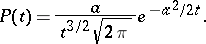 |
Here  , but
, but 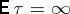 .
.
3) The random variable
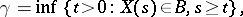 |
being the first time after which  remains in
remains in 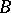 , is an example of a non-Markov moment (a random variable depending on the "future" ).
, is an example of a non-Markov moment (a random variable depending on the "future" ).
Using the idea of a Markov moment one can formulate the strong Markov property of Markov processes (cf. Markov process). Markov moments and stopping times (that is, finite Markov moments) play a major role in the general theory of random processes and statistical sequential analysis.
References
| [1] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) |
Comments
References
| [a1] | R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) |
| [a2] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 |
| [a3] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian) |
| [a4] | A.D. [A.D. Ventsel'] Wentzell, "A course in the theory of stochastic processes" , McGraw-Hill (1981) (Translated from Russian) |
| [a5] | L.P. Breiman, "Probability" , Addison-Wesley (1968) |
Markov moment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_moment&oldid=21656