Markov chain, class of zero states of a

2020 Mathematics Subject Classification: Primary: 60J10 Secondary: 60J27 [MSN][ZBL]

A set 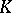of states of a homogeneous Markov chain 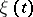with state space such that

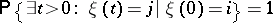for any ,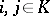

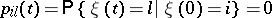for any , , 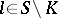, 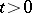and

(*)

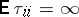for any 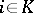, where 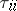is the return time to the state :

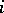for a discrete-time Markov chain, and

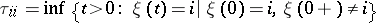for a continuous-time Markov chain.

As in the case of a class of positive states (in the definition of a positive class (*) is replaced by 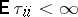), states belonging to the same zero class have a number of common properties. For example, for any states 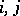of a zero class ,

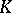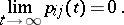An example of a Markov chain whose states form a single zero class is the symmetric random walk on the integers:

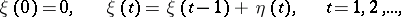where 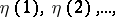are independent random variables,

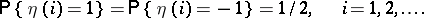References

[1]	K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1967)

Comments

Cf. also Markov chain, class of positive states of a.

References

[a1]	W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1966)
[a2]	D. Freedman, "Markov chains" , Holden-Day (1975)
[a3]	M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980)
[a4]	J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960)
[a5]	J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976)
[a6]	D. Revuz, "Markov chains" , North-Holland (1975)
[a7]	V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian)
[a8]	E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981)