Kolmogorov test
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A statistical test used for testing a simple non-parametric hypothesis 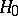 , according to which independent identically-distributed random variables
, according to which independent identically-distributed random variables 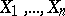 have a given distribution function
have a given distribution function  , where the alternative hypothesis
, where the alternative hypothesis  is taken to be two-sided:
is taken to be two-sided:
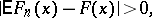 |
where 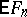 is the mathematical expectation of the empirical distribution function
is the mathematical expectation of the empirical distribution function 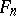 . The critical set of the Kolmogorov test is expressed by the inequality
. The critical set of the Kolmogorov test is expressed by the inequality
 |
and is based on the following theorem, proved by A.N. Kolmogorov in 1933: If the hypothesis 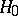 is true, then the distribution of the statistic
is true, then the distribution of the statistic 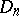 does not depend on
does not depend on 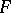 ; also, as
; also, as 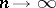 ,
,
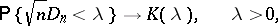 |
where
 |
In 1948 N.V. Smirnov [4] tabulated the Kolmogorov distribution function  . According to the Kolmogorov test with significance level
. According to the Kolmogorov test with significance level  ,
,  , the hypothesis
, the hypothesis 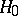 must be rejected if
must be rejected if 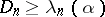 , where
, where  is the critical value of the Kolmogorov test corresponding to the given significance level
is the critical value of the Kolmogorov test corresponding to the given significance level  and is the root of the equation
and is the root of the equation 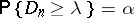 .
.
To determine 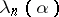 one recommends the use of the approximation of the limiting law of the Kolmogorov statistic
one recommends the use of the approximation of the limiting law of the Kolmogorov statistic  and its limiting distribution; see [3], where it is shown that, as
and its limiting distribution; see [3], where it is shown that, as 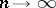 and
and  ,
,
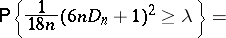 | (*) |
 |
The application of the approximation (*) gives the following approximation of the critical value:
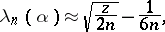 |
where  is the root of the equation
is the root of the equation 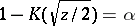 .
.
In practice, for the calculation of the value of the statistic  one uses the fact that
one uses the fact that
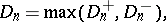 |
where
 |
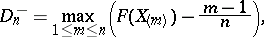 |
and  is the variational series (or set of order statistics) constructed from the sample
is the variational series (or set of order statistics) constructed from the sample  . The Kolmogorov test has the following geometric interpretation (see Fig.).
. The Kolmogorov test has the following geometric interpretation (see Fig.).
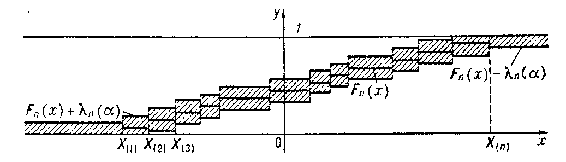
Figure: k055760a
The graph of the functions 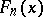 ,
, 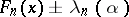 is depicted in the
is depicted in the  -plane. The shaded region is the confidence zone at level
-plane. The shaded region is the confidence zone at level 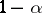 for the distribution function
for the distribution function  , since if the hypothesis
, since if the hypothesis  is true, then according to Kolmogorov's theorem
is true, then according to Kolmogorov's theorem
 |
If the graph of 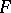 does not leave the shaded region then, according to the Kolmogorov test,
does not leave the shaded region then, according to the Kolmogorov test,  must be accepted with significance level
must be accepted with significance level 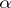 ; otherwise
; otherwise 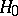 is rejected.
is rejected.
The Kolmogorov test gave a strong impetus to the development of mathematical statistics, being the start of much research on new methods of statistical analysis lying at the foundations of non-parametric statistics.
References
| [1] | A.N. Kolmogorov, "Sulla determinizione empirica di una legge di distribuzione" Giorn. Ist. Ital. Attuari , 4 (1933) pp. 83–91 |
| [2] | N.V. Smirnov, "On estimating the discrepancy between empirical distribiution curves for two independent samples" Byull. Moskov. Gos. Univ. Ser. A , 2 : 2 (1938) pp. 3–14 (In Russian) |
| [3] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theor. Probab. Appl. , 8 (1963) pp. 121–146 Teor. Veroyatnost. i Primenen. , 8 : 2 (1963) pp. 129–155 |
| [4] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
Tests based on 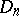 and
and 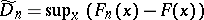 , and similar tests for a two-sample problem based on
, and similar tests for a two-sample problem based on  and
and 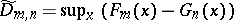 , where
, where  is the empirical distribution function for samples of size
is the empirical distribution function for samples of size  for a population with distribution function
for a population with distribution function 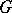 , are also called Kolmogorov–Smirnov tests, cf. also Kolmogorov–Smirnov test.
, are also called Kolmogorov–Smirnov tests, cf. also Kolmogorov–Smirnov test.
References
| [a1] | G.E. Noether, "A brief survey of nonparametric statistics" R.V. Hogg (ed.) , Studies in statistics , Math. Assoc. Amer. (1978) pp. 3–65 |
| [a2] | M. Hollander, D.A. Wolfe, "Nonparametric statistical methods" , Wiley (1973) |
Kolmogorov test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov_test&oldid=21348