Kolmogorov equation
2020 Mathematics Subject Classification: Primary: 60J35 [MSN][ZBL]
An equation of the form
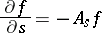 | (1) |
(the inverse, backward or first, equation; 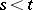 ), or of the form
), or of the form
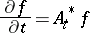 | (2) |
(the direct, forward or second, equation; 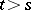 ), for the transition function
), for the transition function 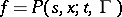 ,
, 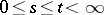 ,
, 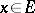 ,
, 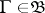 ,
, 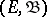 being a measurable space, or its density
being a measurable space, or its density 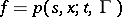 , if it exists. For the transition function
, if it exists. For the transition function  the condition
the condition
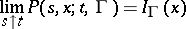 |
is adjoined to equation (1), and the condition
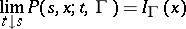 |
is adjoined to equation (2), where 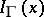 is the indicator function of the set
is the indicator function of the set 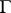 ; in this case the operator
; in this case the operator 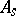 is an operator acting in a function space, while
is an operator acting in a function space, while  acts in a space of generalized measures.
acts in a space of generalized measures.
For a Markov process with a countable set of states, the transition function is completely determined by the transition probabilities 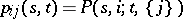 (from the state
(from the state 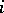 at instant
at instant  to the state
to the state 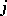 at instant
at instant 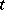 ), for which the backward and forward Kolmogorov equations have (under certain extra assumptions) the form
), for which the backward and forward Kolmogorov equations have (under certain extra assumptions) the form
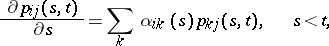 | (3) |
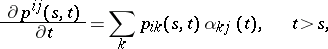 | (4) |
where
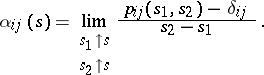 | (5) |
In the case of a finite number of states, equations (3) and (4) hold, provided that the limits in (5) exist.
Another important class of processes for which the question of the validity of equations (1) and (2) has been studied in detail is the class of processes of diffusion type. These are defined by the condition that their transition functions 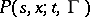 ,
,  ,
, 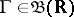 , satisfy the following conditions:
, satisfy the following conditions:
a) for each 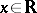 and
and 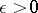 ,
,
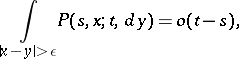 |
uniformly in  ,
, 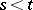 ;
;
b) there exist functions 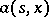 and
and 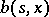 such that for every
such that for every  and
and 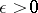 ,
,
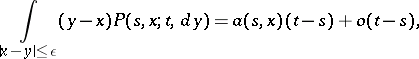 |
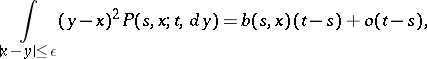 |
uniformly in  ,
,  . If the density
. If the density 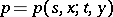 exists, then (under certain extra assumptions) the forward equation
exists, then (under certain extra assumptions) the forward equation
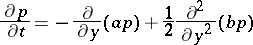 |
holds (for  and
and  ) (also called the Fokker–Planck equation), while the backward equation (for
) (also called the Fokker–Planck equation), while the backward equation (for 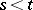 and
and 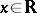 ) has the form
) has the form
 |
References
| [1] | A.N. Kolmogorov, "Ueber die analytischen Methoden in der Wahrscheinlichkeitsrechnung" Math. Ann. , 104 (1931) pp. 415–458 |
| [2] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1979) (Translated from Russian) |
Comments
Besides in a probabilistic context, Kolmogorov equations of course also occur as equations modelling real diffusions, such as the diffusion of molecules of a substance through porous material or the spread of some property through a biological structured population.
See also (the editorial comments to) Einstein–Smoluchowski equation.
References
| [a1] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) |
| [a2] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) pp. Sect. 5.26 (Translated from Russian) |
| [a3] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1966) pp. Chapt. XV.13 |
Kolmogorov equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov_equation&oldid=21347