User:Rafael.greenblatt/sandbox

(starting to modify "Exterior algebra")

Grassmann algebra, of a vector space $V$ over a field $k$

An associative algebra over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of $V$, and with defining relations

$$ e_i \wedge e_j = - e_j \wedge e_i \qquad (i,j=1,\ldots,n), \qquad e_i \wedge e_i = 0, $$

$$ 1 \wedge e_i = e_i \wedge 1 = e_i \qquad (i=1,\ldots,n), \qquad \ \wedge 1 = 1. $$

The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: $ \dim \wedge^r V = () = C_n^r$, $r=0,\ldots,n$, $\wedge^r V =0, $r>n$. In addition, $v \wedge u = (-1)^{rs}u \wedge v$ if $u \in \wedge^r V$, v \in \wedge^s V$. The elements of the space $\wedge^r V$ are said to be $r$-vectors; they may also be regarded as skew-symmetric $r$-times contravariant tensors in $V$ (cf. Exterior product).

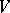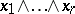-vectors are closely connected with -dimensional subspaces in : Linearly independent systems of vectors and of generate the same subspace if and only if the -vectors and 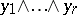are proportional. This fact served as one of the starting points in the studies of H. Grassmann [1], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules over a commutative ring 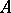with identity [4]. 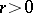The -th exterior power , , of a module is defined as the quotient module of the -th tensor power of this module by the submodule generated by the elements of the form , where and for certain 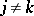. The exterior algebra for 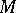is defined as the direct sum , where 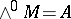, with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [5].

The Grassmann (or Plücker) coordinates of an -dimensional subspace in an -dimensional space 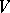over are defined as the coordinates of the -vector in 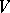corresponding to , which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all -dimensional subspaces in 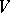into the projective space of dimension 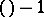, where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].

Exterior algebras are employed in the calculus of exterior differential forms (cf. Differential form) as one of the basic formalisms in differential geometry [7], [8]. Many important results in algebraic topology are formulated in terms of exterior algebras.

E.g., if 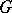is a finite-dimensional 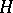-space (e.g. a Lie group), the cohomology algebra 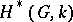of 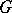with coefficients in a field 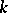of characteristic zero is an exterior algebra with odd-degree generators. If 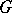is a simply-connected compact Lie group, then the ring 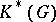, studied in 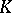-theory, is also an exterior algebra (over the ring of integers).

References

[1]	H. Grassmann, "Gesammelte mathematische und physikalische Werke" , 1 , Teubner (1894–1896) pp. Chapt. 1; 2
[2]	A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)
[3]	L.A. Kaluzhnin, "Introduction to general algebra" , Moscow (1973) (In Russian)
[4]	N. Bourbaki, "Elements of mathematics. Algebra: Multilinear algebra" , Addison-Wesley (1966) pp. Chapt. 2 (Translated from French)
[5]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French)
[6]	W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1–3 , Cambridge Univ. Press (1947–1954)
[7]	S.P. Finikov, "Cartan's method of exterior forms in differential geometry" , 1–3 , Moscow-Leningrad (1948) (In Russian)
[8]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964)

Comments

Anticommuting variables (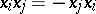, 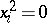) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.

References

[a1]	C. Chevalley, "The construction and study of certain important algebras" , Math. Soc. Japan (1955)