Normal ring

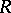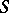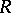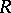Let be a commutative ring with identity and a commutative ring containing , with the same identity element. An element is integral over if there are 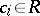such that . The integral closure of in 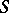is the set of all 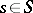which are integral over 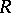. It is a subring 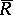of 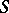containing 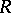. If 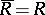, 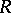is said to be integrally closed in 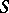(cf. also Integral ring).

A commutative ring with identity 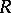is called normal if it is reduced (i.e. has no nilpotents 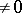) and is integrally closed in its complete ring of fractions (cf. Localization in a commutative algebra). Thus, is normal if for each prime ideal 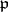the localization 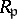is an integral domain and is closed in its field of fractions. In some of the literature a normal ring is also required to be an integral domain.

A Noetherian ring 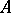is normal if and only if it satisfies the two conditions: i) for every prime ideal 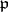of height 1, 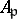is regular (and hence a discrete valuation ring); and ii) for every prime ideal 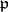of height 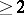the depth (cf. also Depth of a module) is also 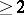. (Cf. [a3], p. 125.)

References

[a1]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)
[a2]	M. Nagata, "Local rings" , Interscience (1962) pp. Chapt. III, §23
[a3]	H. Matsumura, "Commutative algebra" , Benjamin (1970)