Contragredient automorphism
to an automorphism  of a right module
of a right module 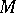 over a ring
over a ring 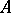
The automorphism  of the left
of the left 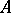 -module
-module 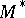 (* denotes taking the dual or adjoint module) that is adjoint to the inverse automorphism to
(* denotes taking the dual or adjoint module) that is adjoint to the inverse automorphism to  . More generally, if
. More generally, if 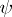 is an automorphism between a right
is an automorphism between a right 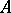 -module
-module 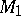 and a right
and a right 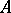 -module
-module 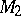 , then the contragredient isomorphism to
, then the contragredient isomorphism to 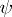 is the isomorphism of the left
is the isomorphism of the left 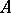 -module
-module 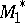 onto the left
onto the left 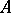 -module
-module 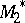 that is adjoint to the inverse of the isomorphism
that is adjoint to the inverse of the isomorphism 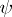 . Let
. Let 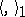 and
and 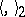 be the canonical bilinear forms on
be the canonical bilinear forms on 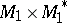 and
and 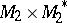 . Then
. Then 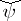 is defined by the following identity with respect to
is defined by the following identity with respect to 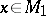 ,
, 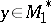 :
:
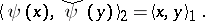 |
If 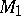 and
and  have finite bases, then
have finite bases, then  is the isomorphism contragredient to
is the isomorphism contragredient to 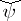 .
.
Let 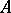 be a ring with an identity, let
be a ring with an identity, let 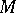 be a right
be a right 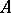 -module with a finite basis, let
-module with a finite basis, let 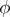 be an automorphism of
be an automorphism of 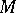 , and let
, and let 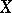 be the matrix of
be the matrix of 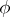 in a fixed basis (this matrix is invertible). Then in the dual basis, the matrix of the contragredient automorphism
in a fixed basis (this matrix is invertible). Then in the dual basis, the matrix of the contragredient automorphism 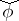 has the form
has the form
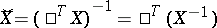 |
(here  denotes the transpose). The matrix
denotes the transpose). The matrix 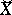 is called the matrix contragredient to the invertible matrix
is called the matrix contragredient to the invertible matrix 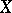 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
Comments
Instead of adjoint module and adjoint automorphism one also uses dual module and dual automorphism (cf. Adjoint module; Automorphism).
Contragredient automorphism. V.L. Popov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contragredient_automorphism&oldid=19201