Hewitt realcompactification

Hewitt compactification, Hewitt extension

An extension of a topological space that is maximal relative to the property of extending real-valued continuous functions; it was proposed by E. Hewitt in [1].

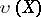A homeomorphic imbedding is called a functional extension if is dense in 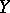and if for every continuous function 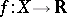there exists a continuous function such that 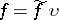. A completely-regular space 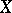is called a 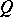-space or a functionally-complete space if every functional extension of it is a homeomorphism, that is, if 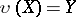. A functional extension 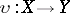of a completely-regular space is called a Hewitt extension if 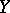is a 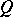-space. A completely-regular space has a Hewitt extension, and the latter is unique up to a homeomorphism.

The Hewitt extension can also be defined as the subspace of those points 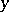of the Stone–Čech compactification 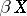for which every continuous real-valued function 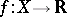can be extended to .

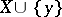References

[1]	E. Hewitt, "Rings of real-valued continuous functions, I" Trans. Amer. Math. Soc. , 64 (1948) pp. 45–99
[2]	R. Engelking, "Outline of general topology" , North-Holland (1968) (Translated from Polish)
[3]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)

Comments

The Hewitt extension is not a compactification, hence the phrase "Hewitt compactification" is rarely used.