Weakly-wandering set
From Encyclopedia of Mathematics
for an invertible measurable transformation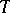 
of a measurable space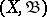 
A measurable subset 
for which there is an infinite sequence of integers 
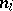such that the sets 
are mutually disjoint (here, invertibility of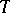 
is understood to mean existence and measurability of 
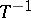). If 
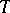has a 
-finite quasi-invariant measure 
(defined on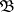 
), then a necessary and sufficient condition for 
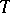to have a finite invariant measure equivalent to 
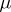is that 
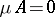for any weakly-wandering set 
.
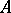A word of warning. In topological dynamics there is a notion of weakly non-wandering point (see [3]) which has nothing to do with the notion defined above.
References
| [1] | A.B. Hajian, S. Kakutani, "Weakly wandering sets and invariant measures" Trans. Amer. Math. Soc. , 110 : 1 (1964) pp. 136–151 |
| [2] | A. Hajian, Y. Itô, "Weakly wandering sets and invariant measures for a group of transformations" J. Math. Mech. , 18 : 12 (1969) pp. 1203–1216 |
| [3] | D.V. Anosov, I.V. Bronshtein, "Topological dynamics" , Dynamical Systems I , Encycl. Math. Sci. , I , Springer (1988) pp. 197–219 (Translated from Russian) |
How to Cite This Entry:
Weakly-wandering set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weakly-wandering_set&oldid=18937
Weakly-wandering set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weakly-wandering_set&oldid=18937
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article