Chernikov group

Černikov group

A group satisfying the minimum condition on subgroups and having a normal Abelian subgroup of finite index (cf. Artinian group; Abelian group; Group with the minimum condition). Such groups have also been called extremal groups. The structure of Abelian groups with the minimum condition was obtained by A.G. Kurosh (see [a4]), who showed that these are precisely the groups that are the direct sum of finitely many quasi-cyclic groups and cyclic groups of prime-power order (cf. Quasi-cyclic group; Group of type 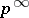). 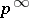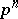A quasi-cyclic group (or Prüfer group of type , for some fixed prime number ) is the multiplicative group of complex numbers consisting of all th roots of unity as runs through the set of natural numbers. It is clear that subgroups and homomorphic images of Chernikov groups are also Chernikov; further, an extension of a Chernikov group by a Chernikov group is again Chernikov.

Chernikov groups are named in honour of S.N. Chernikov, who made an extensive study of groups with the minimum condition. For example, he showed [a1] that a solvable group with the minimum condition on subgroups is (in contemporary terminology) a Chernikov group. Groups with the minimum condition are periodic (cf. Periodic group). In 1970, V.P. Shunkov [a5] proved that a locally finite group with the minimum condition is Chernikov, a result which had been conjectured for many years. In fact, Shunkov's result is stronger: he showed in [a6] that to force the locally finite group to be Chernikov one only needs the condition that all the Abelian subgroups of 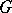have the minimum condition. The first examples of groups with the minimum condition which are not Chernikov were provided in 1979 by A.Yu. Ol'shanskii [a3] and E. Rips. These examples are two-generator infinite simple groups in which every proper subgroup is of prime order .

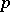Chernikov groups have played an important role in the theory of infinite groups. For example, Chernikov proved that a periodic group of automorphisms of a Chernikov group is also Chernikov (see [a2], 1.F.3) and this fact is used on numerous occasions in the theory of locally finite groups. Many characterizations of Chernikov groups have been obtained. For example, a hypercentral group is a Chernikov group if and only if each upper central factor satisfies the minimum condition (see [a4], Thm. 10.23, Cor. 2).

References

[a1]	S.N. Černikov, "Infinite locally soluble groups" Mat. Sb. , 7 (1940) pp. 35–64
[a2]	O.H. Kegel, B.A.F. Wehrfritz, "Locally finite groups" , North-Holland (1973)
[a3]	A.Yu. Ol'šanskii, "Infinite groups with cyclic subgroups" Dokl. Akad. Nauk SSSR , 245 (1979) pp. 785–787 (In Russian)
[a4]	D.J.S. Robinson, "Finiteness conditions and generalized soluble groups 1–2" , Ergebn. Math. Grenzgeb. , 62/3 , Springer (1972)
[a5]	V.P. Šunkov, "On the minimality problem for locally finite groups" Algebra and Logic , 9 (1970) pp. 137–151 Algebra i Logika , 9 (1970) pp. 220–248
[a6]	V.P. Šunkov, "On locally finite groups with a minimality condition for abelian subgroups" Algebra and Logic , 9 (1970) pp. 350–370 Algebra i Logika , 9 (1970) pp. 579–615